中学３年数学　二次方程式の利用　確認問題4・解答

中学３年数学　二次方程式の利用　確認問題4・解答

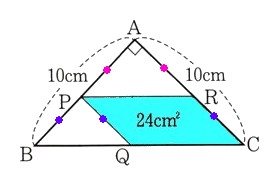
４、ＡB＝ＡC＝１０?の直角二等辺三角形ＡBCがあります。ＡB上の点Pから、ＡC、BCに平行な直線を引きます。BC，ＡCとの交点を、それぞれQ、Rとします。四角形PQCRの面積が２４㎠になるとき，ＡPの長さを求めてください。

まずは、この四角形の面積をどうすれば求められるかを考えます。

全体の三角形ＡBCから、小さい２つの三角形ＡPRとPBQを除けば四角形の面積２４㎠がわかります。

?大きな三角形の面積はＡB×ＡC÷２ですから

１０?×１０?÷２＝５０㎠・・・?

ＡPの長さをχ?として考えると、

PBの長さは（１０ーχ）?となります。

?三角形ＡPRの面積は
BC//PRなので、ＡP＝ＡRになります。

ＡPの長さはχ?ですから

ＡRの長さもχ?になります。

△ＡPRの面積はχ×χ÷２＝χ²／２㎠

?三角形PBQの面積は

BC//PRなので、PB＝RCになります。

PBの長さは（１０ーχ）?ですから

RCの長さは（１０ーχ）?になります。

△PBQの面積は（１０ーχ）×（１０ーχ）÷２＝（１０ーχ）²／２

四角形を出す式をつくります

５０㎠ーχ²／２㎠ー（１０ーχ）²／２㎠＝２４㎠

両辺に２を掛けます。

１００ーχ²ー（１０ーχ）²＝４８

（１０ーχ）²を展開します。

●（ａーｂ）²＝ａ²ー２ａｂ＋b²

（１０ーχ）²＝１０²ー２×１０×χ＋χ²

＝１００ー２０χ＋χ²

１００ーχ²ー（１００ー２０χ＋χ²）＝４８

１００ーχ²ー１００＋２０χーχ²＝４８

χ²＋χ²ー２０χー１００＋１００＋４８＝０

２χ²ー２０χ＋４８＝０

両辺を２で割ります。

χ²ー１０χ＋２４＝０

かけて２４、たしてー１０になる２つ数は

（−４）×（−６）＝２４，（−４）＋（−６）＝ー１０

χ²ー１０χ＋２４＝（χー４）（χー6）

χ²ー１０χ＋２４＝０
       ですから
     （χー４）（χー6）＝０

Ａ×B＝０ならば　Ａ＝０　または　B＝０になります。

（χー４）＝０、（χー6）＝０

χ＝４　　、　χ＝６

になります。

どちらも、条件に合いますから、

答え　ＡP＝４?、６?