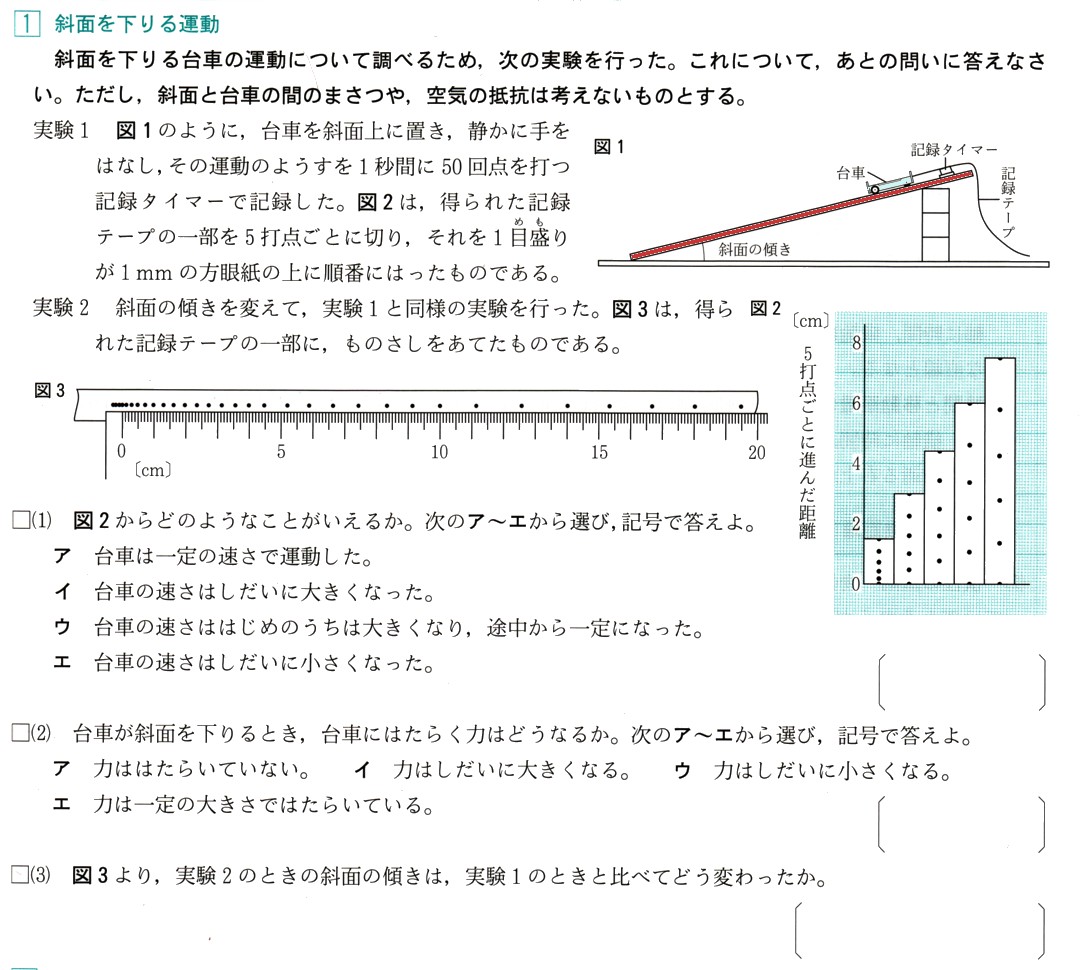
中学3年数学 関数y=aχ²の値の変化 練習問題7・解答
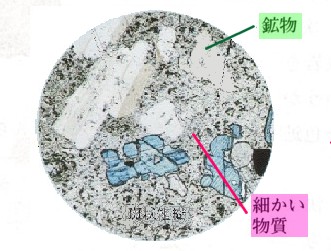
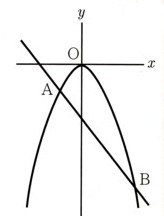
7、図 のように、放物線y=aχ²と直線y=bχ−4が2点A,Bで交わっています。点A,Bのχ座標がそれぞれ−1,2であるとき、次の問いに答えてください。
のように、放物線y=aχ²と直線y=bχ−4が2点A,Bで交わっています。点A,Bのχ座標がそれぞれ−1,2であるとき、次の問いに答えてください。
(1)a、bの値を求めてください。
2つの点A,Bをy=aχ²とy=bχ−4で考えます。
y=aχ² に−1を代入します。
y=a1²
y=a
y=aχ² に2を代入します。
y=a2²
y=4a
y=aχ²では(χ、y)=点A(−1、a)点B(2、4a)
y=bχ−4 に−1を代入します。
y=b(−1)−4=−b−4
y=bχ−4 に2を代入します。
y=b2−4=2b−4
y=bχ−4では(χ、y)=点A(−1、−b−4)点B(2、2b−4)
になります。
これで、2つの点A,Bのy座標がでました。
点A(y=a) 点B(y=4a) ・・・?
点A(y=−b−4)点B(y=2b−4)・・・?
?,?を連立方程式にしてa、bを求めます。
a=−b−4
{
4a=2b−4
(代入法)で考えます。
4×(−b−4)=2b−4
−4b−16=2b−4
−4b−2b=−4+16
−6b=12
b=−12/6
b=−2
a=−b−4にb=−2を代入します。
a=−(−2)−4
a=2−4
a=−2
答え a=−2、b=−2
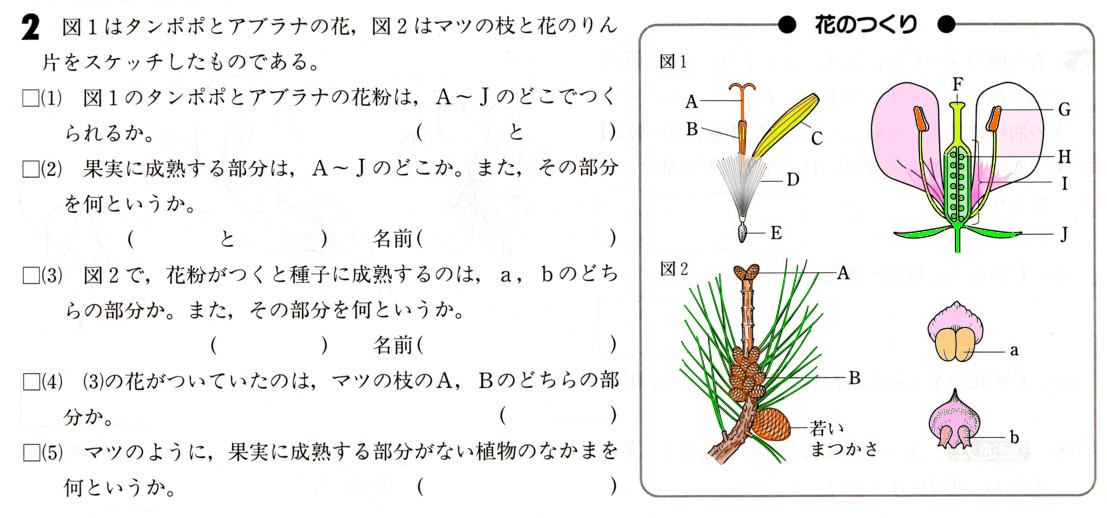
(2)Oを通り、△OABの面積を2等分する直線の式を求めてください。
△OABの面積を2等分する直線とは、ABの中点から点Oを結ぶ直線となります。
まずは、(1)で点A,点Bの座標がわかりますから、中点を考えます。
y=−2χ−4にχ=−1、χ=2を代入します。
y=−2×(−1)−4 、y=−2×2−4
=2−4 、 =−4−4
=−2 、 =−8
点A(−1、−2)、点B(2、−8)となります。
点A、点Bのχ座標の半分がχ座標の中点になります。
点A、点Bのy座標の半分がy座標の中点になります。
−1+2 1 −2−8 −10
――― =― 、――――=――=−5
2 2 2 2
(χ、y)=(1/2、−5) が中点となります。
直線の式になりますから一次関数の式になります。原点Oを通りますから切片はありません。
y=aχ の式に(χ、y)=(1/2、−5)を代入します。
−5=1/2a
1/2a=−5
a=2×(−5)
a=−10
傾き(a)が−10とわかりましたから、y=aχの式にあてはめます。
y=−10χ
答え y=−10χ









コメント