中学1年数学　空間図形　まとめテスト６　解答・解説

中学1年数学　空間図形　まとめテスト６　解答・解説

　　次の問いに答えてください

（１）底面が1辺8cmの正方形で、側面の二等辺三角形の高さが6cmである正四角錐の表面積

　　を求めてください。

　　　　正四角錐ということは、底面が、正方形で、側面は二等辺三角形ですから。

　　正方形の面積は、1辺が8cmですから

　　(正方形の面積)＝8cm×8cm＝64?²

　　（二等辺三角形の面積）＝8×6×1/2＝24cm²

　　　側面は4面ありますから

　　　　　　　24cm²×4＝96?²

　　(正四角錐の表面積)＝(底面積)＋(側面積)

　　　　　　　　　　　＝(64?²)＋(96?²)

　　　　　　　　　　　＝160cm²

　　　答え　160?²

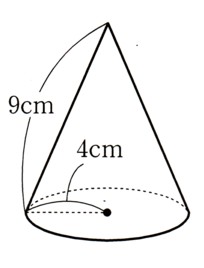
（２）図のような、底面の半径が4cm、母線の長さが9cmの円錐について、側面の展開図の

　　おうぎ形の中心角と表面積をそれぞれ求めてください。

　　　円錐の表面積は、

　　　(円錐の表面積)＝(底面積)＋(側面積)

　　　(底面積)＝(半径4cm円の面積)＝4×4×π

　　　　　　　　　　　　　　　　　＝16πcm²

　　　(側面積)＝(おうぎ形の面積)＝9×9×π×中心角/360

　　　　　　　　　　　　　　　　＝81π×中心角/360

　　　中心角の角度は、まだわかりませんから、底面の円の円周とおうぎ形の弧の長さは

　　等しくなりますから。

　　　(おうぎ形の弧の長さ)＝(底面の円の円周)

　　　(2πγ×中心角/360)＝(2πγ)

　　　(2×9×π×中心角/360)＝(2×4×π)

　　　(18π×中心角/360)＝(8π)

　　　両辺に360/18πをかけます

　　　360/18π×(18π×中心角/360)＝360/18π×(8π)

　　　　中心角＝360/18π×(8π)

　　　　　　　＝160゜

　　　　(おうぎ形の面積)＝81π×中心角/360

　　　　　　　　　　　　＝81π×160/360

　　　　　　　　　　　　＝36πcm²

　　　(円錐の表面積)＝(底面積)＋(側面積)

　　　　(底面積)＝16πcm²

　　　　(側面積)＝36πcm²

　　　(円錐の表面積)＝16πcm²＋36πcm²

　　　　　　　　　　＝52π?²

　　　　答え　　中心角　160゜、表面積　52π?²