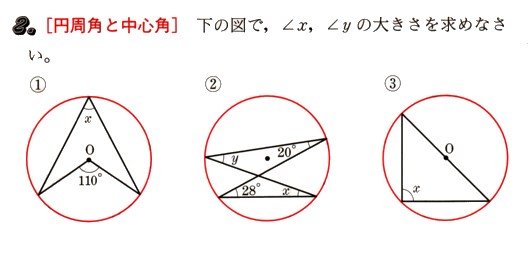
中学3年数学 二次方程式
1、二次方程式とその解き方
●二次方程式
移項して整理すると、(χの二次式)=0の形になる方程式を、χについての二次方程式といいます。
一般の形は、
aχ²+bχ+c=0
と書くことができます。
●二次方程式にあてはまる文字の値を、その方程式の解といいます。解をすべて求めることを二次方程式を解くといいます。
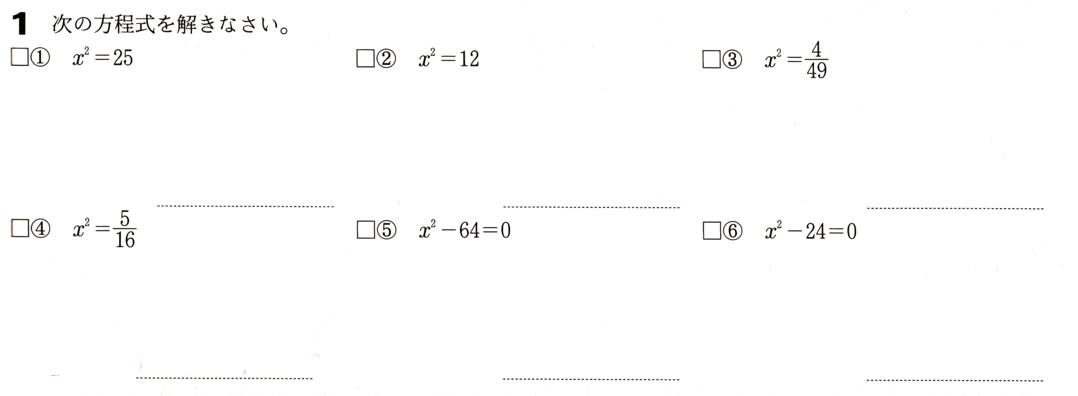
●aχ²=bの解き方
aχ=bの形の方程式は、χ²=kの形に変形すれば、平方根の意味に基づいて解くことができます。
●(χ+m)²=nの解き方
χ+m=Xとおくと、X²=nとなり、aχ²=bと同じ方法で解くことができます。
●χ²+pχ+q=0の解き方
χの一次の項を含む二次方程式は、(χ+m)²=nの形に変形して解くことができます。
2、二次方程式と因数分解
●A×B=0ならば、A=0またはB=0となります。
●(χ+a)(χ+b)=0の解
χ+a=0またはχ+b=0ですから、χ+a=0のとき
χ=ーa、χ+b=0のとき、χ=ーbが解となります。





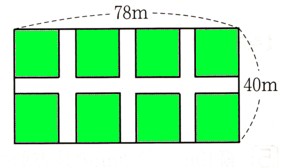
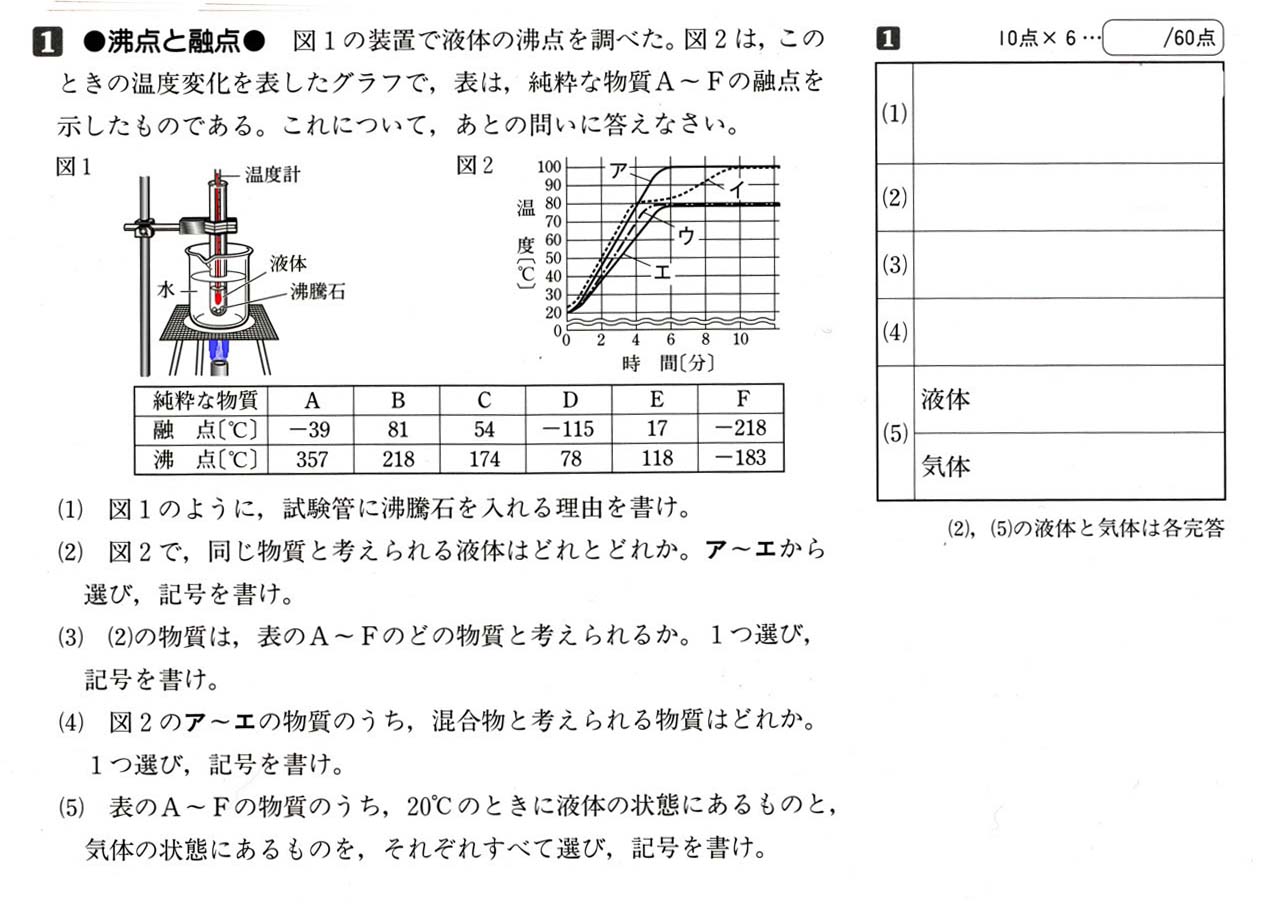


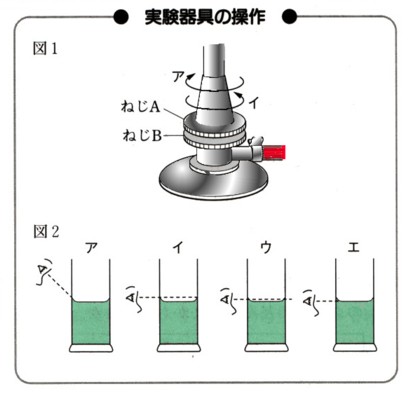



コメント