中学3年数学 変化の割合の計算、交点の座標 確認問題1・解答
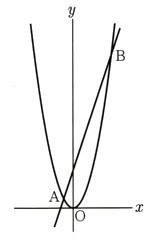
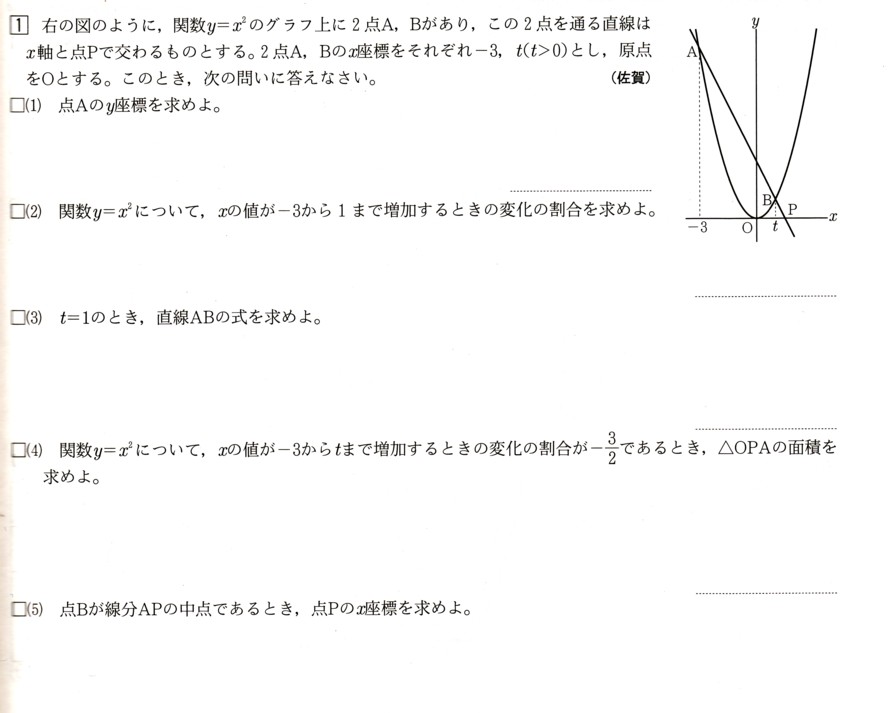
1、図 のように、関数y=χ²のグラフ上に2点A,Bがあります。この2点を通る直線は
のように、関数y=χ²のグラフ上に2点A,Bがあります。この2点を通る直線は
χ軸と点Pで交わるものとします。2点A,Bのχ座標をそれぞれー3、t(t>0)とし、
原点をOとします。このとき、次の問いに答えてください。
(1)点Aのy座標を求めてください。
点Aのχの座標は−3ですから、y=χ²にχ=−3を代入します。
y=(−3)²
=9
答え 9
A座標(−3,9)
(2)関数y=χ²について、χの値がー3から1まで増加するときの変化の割合を求めてください。
関数y=aχ²の変化の割合は、χの値がpからqまで増加するとき、
変化の割合=a(p+q)で求めることができます。
1(−3+1)=1×−2=−2
変化の割合は−2になります。
答え −2
(3)χ=1のとき、直線ABの式を求めてください。
y=χ²にχ=1を代入します。
y=1
直線の式はy=aχ+b ですから、
1=1a+b
y=χ²の変化の割合と直線の傾きは等しくなりますから、(2)でy=χ²の変化の割合は−2
ですから、直線1=1a+bの傾き(a)は−2となります。
1=−2+b
b=1+2
b=3
切片が3となります。
この直線の式は y=−2χ+3
答え y=−2χ+3
(4)関数y=χ²について、χの値がー3からtまで増加するときの変化の割合が−3/2であるとき、
 △OPAの面積を求めてください。
△OPAの面積を求めてください。
関数y=χ²の変化の割合が−3/2であるならば、ABを結ぶ直線の式の傾きは−3/2であるということになり、
y=−3/2χ+b になります。
この直線の式に点Aの座標(−3,9)を代入します。
9=−3/2×(−3)+b
9=9/2+b
b=9−9/2
b=18/2−9/2
b=9/2
切片が9/2 とわかり、この式は
y=−3/2χ+9/2
になります。
つぎに、点Pの座標を考えます。
直線のy=−3/2χ+9/2にy=0を代入します。
0=−3/2χ+9/2
−3/2χ=−9/2
χ=9/2×2/3
χ=18/6=3
点P座標は(3,0)になります。
これで三角形OPAの底辺OP(点Pのχ座標3)で高さ点Aのy座標(9)になり
3×9÷2=27/2
答え 27/2
(5)点Bが線分APの中点であるとき、点Pのχ座標を求めてください。
まずは、点Bの座標を求めます。
放物線ABの式はy=χ² ですから
点Bのχ座標をmとしたとき、yの座標は
y=(m)² になります。
これで、点Bの座標は(m、m²)になります。
そして、点Bは直線APの中点ですから、
χの増加量 yの増加量
χ座標=―――― 、y座標=―――――
&nbs
p; 2 2
−3+p 9+0
m=―――、m²=―――
2 2
9
m²=――
2
√9 √9×√2 3√2
m=――=―――――=――
√2 √2×√2 2
点Bの座標は(3√2/2、9/2)になります。
点Pのχの座標は、点Aのχ座標+点Bのχ座標×2になります。
点Aのχ座標=−3 (原点からの長さは3)
点Bのχ座標=3√2/2 (原点からの長さは3√2/2)
3+3√2
――――×2=3+3√2
2
点Pのχ座標は3+3√2になります。
答え 3+3√2





コメント