中学3年数学 三平方の定理の利用 3確認問題2・解答
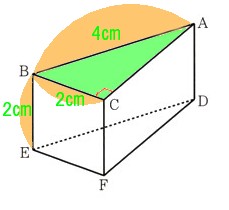
2、次の図 は、BC=BE=2?、AB=4?、∠ACB=90゜の三角柱ABCDEFになります。
は、BC=BE=2?、AB=4?、∠ACB=90゜の三角柱ABCDEFになります。
このとき次の問いに答えてください。
(1)辺ACの長さを求めてください。
△ABCで考えます。
∠ACB=90゜ですから、直角三角形になります。
三平方の定理を利用します。
(底辺)²+(高さ)²=(斜辺)²
底辺=BC=2cm
高さ=AC=χ?
斜辺=AB=4?
(2)²+(χ)²=(4)²
4+χ²=16
χ²=16−4
χ²=12
χ=√12(χは+になります)
χ=2√3?
答え AC=2√3?
(2)3点B,D,Fを頂点とする△BDFの面積を求めてください。
まずは、△BEFで三平方の定理を使い考えます。
(底辺)²+(高さ)²=(斜辺)²
底辺=EF=2cm
高さ=BE=2cm
斜辺=BF=χ?
(2)²+(2)²=(χ)²
4+4=χ²
χ²=8
χ=√8(χは+になります)
χ=2√2?
BF=2√2?・・・?

次に、△BFDで∠BFD=90゜ですから
△BFDの面積=(底辺)×(高さ)×1/2
底辺=BF=2√2?・・・?より
高さ=DF=2√3cm・・・(1)より
2√2×2√3×1/2=4√6/2=2√6㎠
答え 2√6㎠
(3)3点B,D,Fを含む平面と点Eとの距離を求めてください。
△BFDを底辺として考えると高さは点Eから辺BFに垂線を下ろして交わる点をGとします。
この点Gから点Eまでの距離が三角錐E−BFDの高さになります。
△EBGを三平方の定理を使い考えます。
底辺=EG=χcm
高さ=BG=2√2×1/2=√2cm
斜辺=BE=2cm
(底辺)²+(高さ)²=(斜辺)²
(χ)²+(√2)²=(2)²
χ²+2=4
χ²=4−2
χ²=2
χ=√2
EG=√2cm
答え √2?









コメント