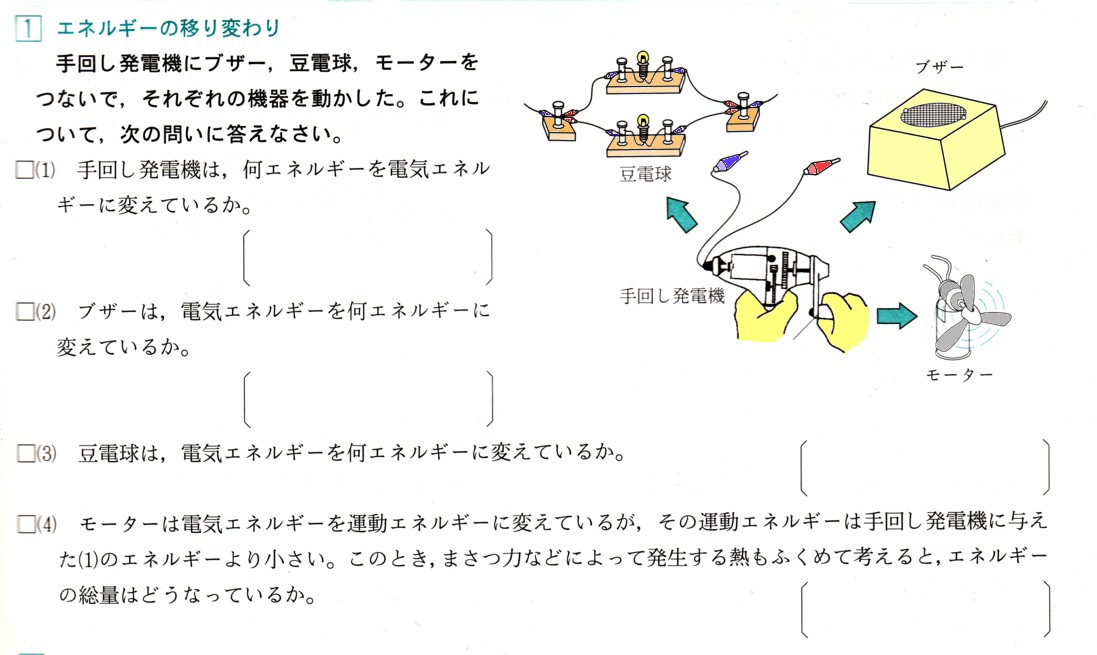
確認問題3(方程式の利用)解答・解説
弟は駅に向かって家を出発し、毎分40mの速さで進みました。兄は、弟より
6分遅れて家を出発し、同じ道を追いかけました。次の問いに答えてください。
(1)兄が家を出発してから12分後に、駅への途中で、弟に追いつきました。
兄の速さは毎分何mになりますか?ただし2人はそれぞれ一定の速さで進む
ものとします。
まずは整理します
●→ → → → → → △
(家) (駅)
弟は、分速40mで進む
兄は、6分遅れで出発
この時点で弟は、道のり=速さ×時間
40 6分
240m先にいます。
同じ道のりで追いつくのですから、同じ距離を進んだことになります。
(弟が進んだ距離)=(兄が進んだ距離)
12分後に弟に追いついたということは、弟の進んだ距離は、
(最初に進んでいた距離)+(12分間進んだ距離)=(弟が進んだ距離)
240m +12(分)×40(速さ)
240+480=720(m)
弟が進んだ距離が720メートルということがわかりました
(弟が進んだ距離)=(兄が進んだ距離)ですから
(兄が進んだ距離)も720mだということがわかります。
兄の速さをχで式を表してみます
(兄が進んだ距離)=(兄の速さ)×(兄の時間)
720(m) = χ × 12(分)
720=12χ
両辺に1/12をかけます
1/12×720=1/12×12χ
60=χ
兄の速さは 分速 60m ということがわかりました
答え 分速 60m
(2)もし兄が(1)で求めた速さの2倍の速さで弟を追いかけたとすると、兄は
家を出発してから何分後に追いつきますか?ただし、2人はそれぞれ一定の
速さで進むものとします。
この問題も、兄が弟に追いつくということは、兄と弟が同じ時間、
同じ距離を進んだということになります。
兄の速さは1の場合の2倍ということは
60m×2=120m 分速120m
まず、弟は、分速40mで進む
兄は、6分遅れで出発
この時点で弟は、道のり=速さ×時間
40 6分
240m先にいます。
同じ道のりで追いつくのですから、同じ距離を進んだことになります。
(弟が進んだ距離)=(兄が進んだ距離)
(弟が進んだ距離)=(弟が6分前に進んだ距離)+(速さ×時間)
速さは、わかっていますから、時間をχで考えます。
速さは、40(m)×時間は、χ(分)
(弟が進んだ距離)=(弟が6分前に進んだ距離)+(速さ×時間)
= 240(m) +40(m)×χ(分)
= 240+40χ
次に、兄の進んだ距離を考えていきましょう。
(兄の進んだ距離)=(速さ)×(時間)
=120(m)×χ(分)
(弟が進んだ距離)=(兄が進んだ距離)
(240+40χ)=(120χ)
120χ=240+40χ
右辺の40χを移項して符号を変えます
120χ−40χ=240
80χ=240
両辺に1/80をかけます
1/80×80χ=1/80×240
χ=3
χは、時間ですから。
χ=3(分)
答え 3分後に追いつく











コメント