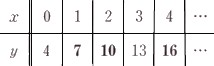
中学2年数学　式の計算　式の利用　練習問題1・解答

１、文字式の利用

　　3桁の自然数で、各位の数の和が3の倍数になるとき、その自然数は3の倍数であることを、次のように説明しました。空欄に適当な数、式を入れてください。

【説明】

　　3桁の自然数の百の位の数をχ、十の位の数をy、一の位の数をzとすると、

　　100χ＋10y＋z＝(ｱ[　 ]＋1)χ＋(9＋1)y＋z

　　　　　　　　　＝ｱ[　 ]χ＋9y＋χ＋y＋z

　　　　　　　　　＝3(ｲ[　 ]χ＋3y)＋(χ＋y＋z)

　　　ｲ[　 ]χ＋3yは整数ですから、ｳ[ 　]は3の倍数、条件より　χ＋y＋z　は3つの倍数ですから、100χ＋10y＋zは、ｴ[　 ]の倍数である。

100χ＋10y＋z＝(ｱ[　99]＋1)χ＋(9＋1)y＋z

　　　　　　　　　＝ｱ[　99]χ＋9y＋χ＋y＋z

　　　　　　　　　＝3(ｲ[　33]χ＋3y)＋(χ＋y＋z)

　　　ｲ[33]χ＋3yは整数ですから、ｳ[3(33+3y)]は3の倍数、条件より　χ＋y＋z　は3の倍数ですから、100χ＋10y＋zは、ｴ[3]の倍数である。

3桁の自然数100χ＋10y＋z　の各位の数の和χ＋y＋z　が3の倍数であるとき、この3桁の自然数は3の倍数になることを説明しているのですから、

　　100χ＋10y＋z＝3×(整数)＋(χ＋y＋z)
　　　　　　　　　　　　　　　↓　　　　　　↓
　　　　　　　　　　　　　　3の倍数　　3の倍数

　　　の形にすればいいということになります。

　　　答え　ア　99　、イ　33　、ウ　3(33+3y)　、エ　3