中学1年数学　立体の表面積と体積　練習問題3　解答・解説

次の立体の体積を求めてください

（１）底面の1辺の長さが10cmで、高さが6?の正四角錐。

　　錐の体積の求める式は

　　　V＝1/3Sｈ

　　(錐の体積)＝1/3×(底面積)×(高さ)

　　底面の形は正四角錐の場合は正方形になります。

　　　(底面積)＝(正方形の面積)

　　正方形の面積の求める式は

　　4辺がそれぞれ等しい辺になりますから

　　(1辺)×(1辺)＝(正方形の面積)

　　1辺の長さは、10cmですから

　　10×10＝100cm²

　　(底面積)＝100cm²

　　　次に高さは、6cmですから

　　(錐の体積)＝1/3×(底面積)×(高さ)

　　　　　　　＝1/3×100cm²×6cm

　　　　　　　＝200cm³

　記号を忘れずに

　　　答え　200cm³

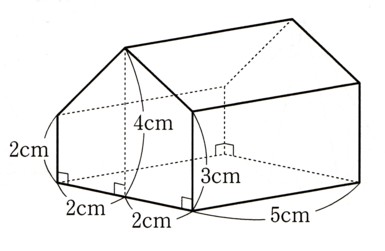
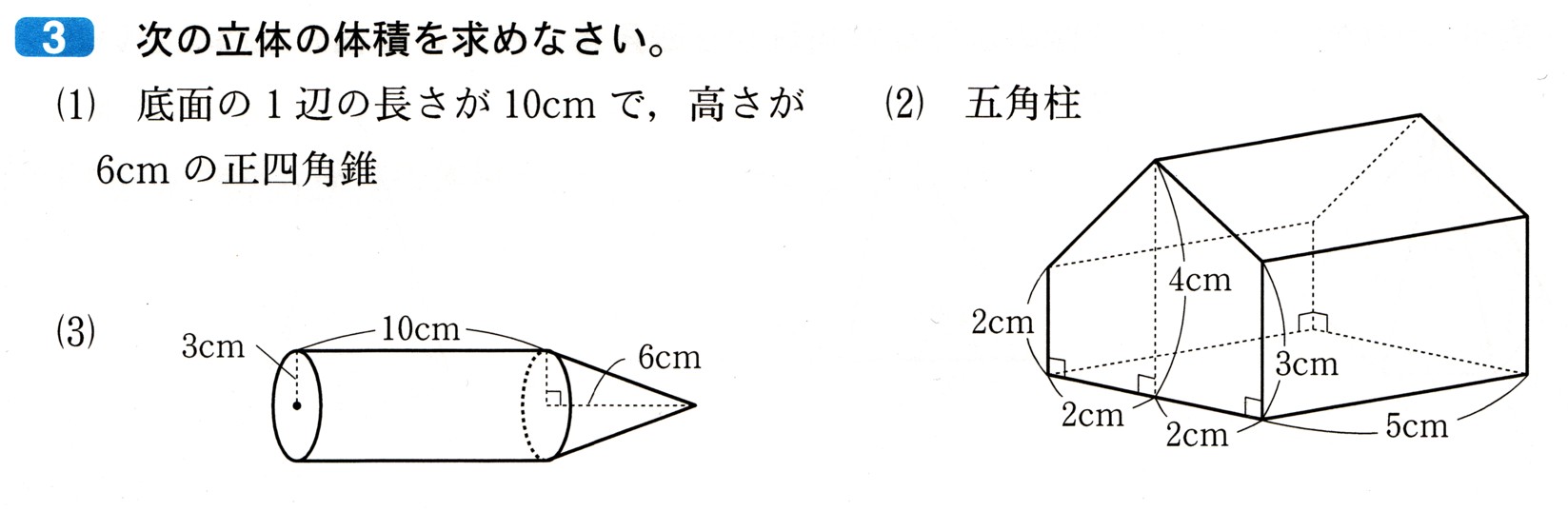
（２）五角柱

　　図

　　　柱の体積の求める式は

　　V＝Sｈ

　　　(柱の体積)＝(底面積)×(高さ)

　　今回の底面は、5角柱ですが、これでは、わかりにくいので

　　底面を半分に分けて考えます

　　そうすると、２つの台形になります。

　　?(上底2cm)、(下底4cm)、(高さ2cm)

　　?(上底3cm)、(下底4cm)、(高さ2cm)

　　台形の面積を求める式は

　　(台形の面積)＝(上底＋下底)×高さ×1/2

　　になります。

　　それでは?,?の面積を求めていきます。

　　(台形の面積)＝(2＋4)×2×1/2

　　　　　　　　＝6×2×1/2

　　　　　　　　＝12×1/2

　　　　　　　　＝6cm²

　　(台形の面積)＝(3＋4)×2×1/2

　　　　　　　　＝7×2×1/2

　　　　　　　　＝14×1/2

　　　　　　　　＝7?²

　　(底面積)＝(?の台形の面積＋?の台形の面積)

　　(底面積)＝6cm²＋7?²

　　　　　　＝13?²

　　　(柱の体積)＝(底面積)×(高さ)

　　　高さは、5cmですから

　　　(柱の体積)＝13?²×5cm

　　　　　　　　＝65?³

　　　　答え　65?³

（３）

この図形は、2つに分けて考えましょう

　　?円柱

　　?円錐

　　　の合わさった図形と考えます

　　?から考えていきましょう

　　円柱の体積の求める式は

　　　V＝Sｈ

　　(円柱の体積)＝(底面積)×(高さ)

　　(底面積)＝(円の面積)　ですから

　　円の面積を求める式は

　　(円の面積)＝πγ²

　　　　　　　＝(半径)×(半径)×π

　　半径は、3cmですから

　　　　　　　＝3×3×π

　　　　　　　＝9πcm²

　　円柱の高さは10cmになりますから

　　(円柱の体積)＝(底面積)×(高さ)

　　　　　　　　＝9πcm²×10cm

　　　　　　　　＝90πcm³

　　つぎに、?の円錐の面積を求めます

　　円錐の体積を求める式は

　　(円錐の体積)＝1/3Sｈ

　　　　　　　　＝1/3×(底面積)×(高さ)

　　底面積は、円柱の底面積と同じになりますから、9πcm²

　　高さは、6cmになります。

　　　　　　　　＝1/3×9πcm²×6cm

　　　　　　　　＝18?³

　　(この立体の体積)＝(円柱の体積)＋(円錐の体積)

　　　　　　　　　　＝90πcm³＋18?³

　　　　　　　　　　＝108?³

　　　答え　　108?³