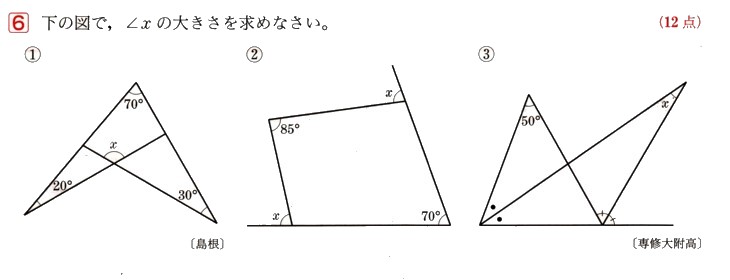
中学2年数学 式の計算 まとめテスト8・解答
8、一の位が0でなく、十の位の数と一の位の数が異なる2桁の自然数Aがあり、Aの十の位の数と一の位の数を入れ替えてできる2桁の整数をBとします。AとBの和を次の例で調べたところ、11の倍数となりました。
(例) 63+36=99=11×9
このとき、次の問いに答えてください。
(1)上の例以外の数についても、和が11の倍数になることを確かめたい。例に習って、1つ書いてください。
【解答例】
52+25=77=11×7
11×(整数)で11の倍数ということがわかります。
(2)Aの十の位の数をχ、一の位の数をyとして、A+Bが11の倍数になることを説明してください。
【解答・解説】
A: 10の位を 10χとし
1の位を yとします。
(10χ+y)になります。
B: 10の位を 10yとし
1の位を χとします。
(10y+χ)になります。
これをA+Bの式に代入します。
(10χ+y)+(10y+χ)
( )をはずします。
=10χ+y+10y+χ
同類項にまとめます。
=10χ+χ+10y+y
=11χ+11y
=11(χ+y)
χ+y は整数ですから、
11(整数)
χ+y は
11の倍数ということがわかります。












コメント