中学2年数学　連立方程式　連立方程式の応用　練習問題1・解答

中学2年数学　連立方程式　連立方程式の応用　練習問題1・解答

１、代金・個数の問題

　「1個80円のパンと1個200円のケーキを合わせて13個買い、代金1640円を払いました。それぞれ何個買いましたか？」

　　この問題を次のようにして解きました。［　　　］にあてはまるものを答えてください。

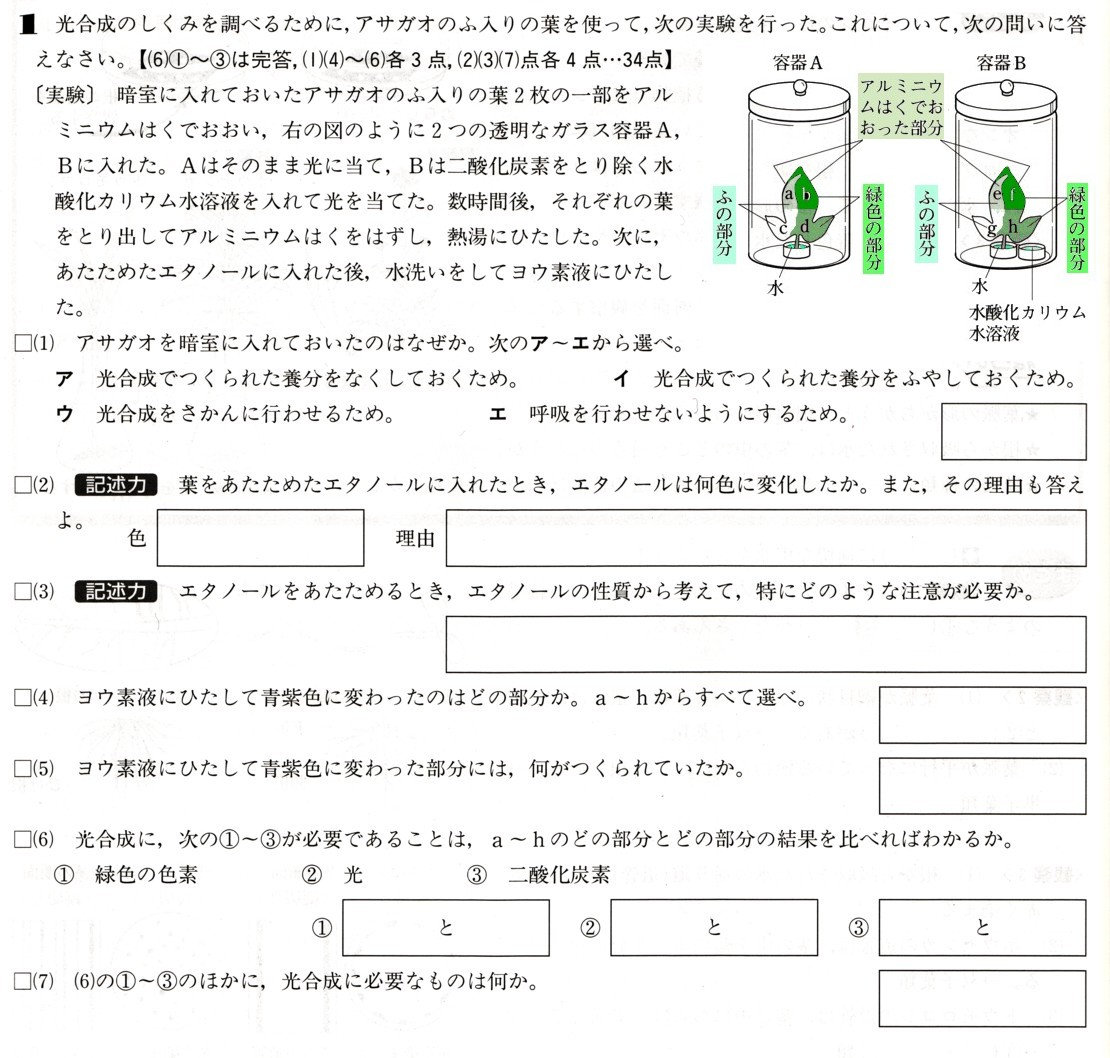
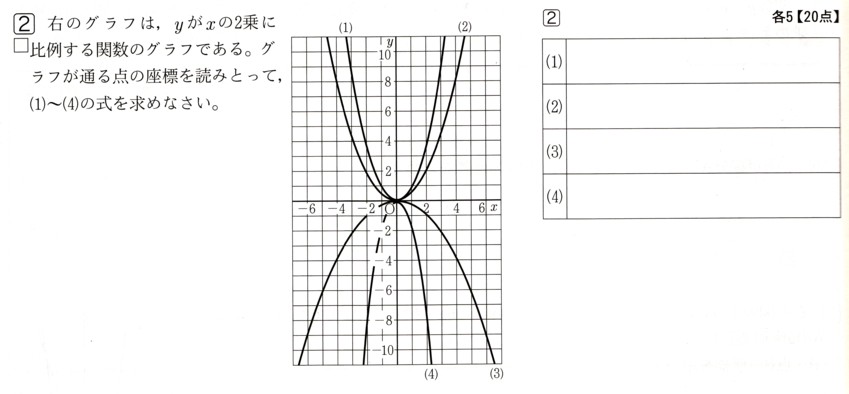
　　　1個80円のパンをχ個、1個200円のケーキをy個買うとします。

　　個数の関係で、(パン)＋(ケーキ)＝13(個)　ですから

　　個数の関係から、［ｱ　χ＋y　］＝13　　・・・?

　　代金の関係で、(単価)×(個数)＝1640(円)　になります、

　　パンの代金は、(80)円×(χ)個＝(80χ)円、になり、ケーキの代金は、(200)円×(y)個＝(200y)円になります。

　　代金の関係から、［ｲ　80χ＋200y　］＝1640　・・・?
　　　
　　　　χ＋y　＝13
　　　｛
　　　　80χ＋200y　＝1640

　　　　χ＋y　＝13　を　y　＝～　の形にします。

　　　　y　＝13−χ

　　　　80χ＋200y　＝1640　に　y　＝13−χ　を代入します。

　　　　80χ＋200（13−χ）　＝1640

　　　　80χ＋2600−200χ　＝1640

　　　　80χ−200χ　＝1640−2600

　　　　−120χ　＝−960

　　　　　　χ＝8

　　　　χ＋y　＝13　に　χ＝8　を代入します。

　　　　8＋y　＝13

　　　　y　＝13−8

　　　　y　＝5

　　?．?を連立方程式として解くと、χ＝［ｳ　8　］、y＝［ｴ　5　　］

　これらは、問題の答えとして、適している。

　　答は、80円のパンは［ｳ　8　］個、200円のケーキは［ｴ　5　　］個。

　　　　答え　ア、χ＋y　イ、80χ＋200y　ウ、8　エ、5