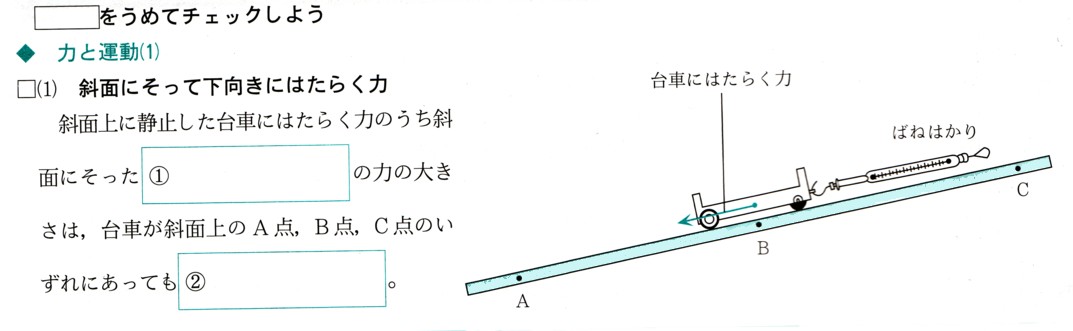
中学2年数学　1次関数　1次関数の応用　確認問題３(2)・解答

中学2年数学　1次関数　1次関数の応用　確認問題３(2)・解答

（２）直線ＡＣと直線ＯＢの交点の座標を求めて下さい。

       直線ＡＣのＡ点の座標(4,0)

　　　Ｃ点の座標は、まだわかりませんから線分ＯＣ（ｙ＝2χ）、ＣＢ（ｙ＝3）の式で考えます。

　　　2直線の交点が点Ｃの座標になります。

　　　　　ｙ＝2χ
　　　｛
　　　　　ｙ＝3

　　　2χ＝3

　　　χ＝3/2

　　ｙ＝2χ　に　χ＝3/2　を代入します。

　　ｙ＝2×3/2　

　　ｙ＝3

　　　点Ｃの座標がわかりました。Ｃ (3/2,3)

　　これで、Ａ座標(4,0)、Ｃ座標(3/2,3)がわかりました。

　　2元1次方程式で考えます。

　　　　0＝4ａ＋ｂ
　　｛
　　　　3＝3/2ａ＋ｂ

　　　　 8/2ａ＋ｂ　＝0
　−)　 3/2ａ＋ｂ　＝3
           5/2ａ      ＝−3

   ａ＝−3×2/5

　　ａ＝−6/5　

　　0＝4ａ＋ｂ　に　ａ＝−6/5　を代入します。

　　0＝4（−6/5）＋ｂ
　
　　　4（−6/5）＋ｂ＝0

　　　−24/5 ＋ｂ＝0

　　　ｂ＝24/5

　　　ａは(傾き)で、ｂは(切片)になりますから。

　　ｙ＝(傾き)χ+(切片)

　　ｙ＝−6/5χ＋24/5・・・・線分ＡＣの式

　　　線分ＯＢの式は、点Ｂ　の座標は（11/2、3）ですから、

　　3＝11/2ａ

　　11/2ａ＝3

　　　ａ＝3×2/11

　　　ａ＝6/11

　　　(切片)は原点から始まっていますから、つきません。

　　　ｙ＝6/11χ　・・・・線分ＯＢの式

　　　2つの直線の交点が座標になります。

　　　　ｙ＝−6/5χ＋24/5
　　｛
　　　　ｙ＝6/11χ

　　　　　6/11χ＝−6/5χ＋24/5

　　　6/11χ＋6/5χ＝24/5

　　　30χ/55＋66χ/55＝264/55

　　　30χ＋66χ＝264

　　　96χ＝264

　　　χ＝11/4

　　　ｙ＝6/11χ　に　χ＝11/4　を代入します。

　　　ｙ＝6/11×11/4

　　　ｙ＝66/44

　　　ｙ＝3/2

　　線分ＯＢ，ＡＣの交点がわかりました。

　　　答え　(χ．ｙ)＝（11/4、3/2）

　別解 

　　平行四辺形の対角線は,それぞれの中点で交わりますから、線分ＯＢの中点がわかれば、中点になります。

 線分ＯＢは、原点(0,0)、座標Ｂ（11/2、3）ですから、

　　　　  (11/2−0)　(3−0)
　　　　―――――,―――　になります。
　　　　　  　２　　      　２

     ＝11/4、3/2