中学2年数学 1次関数 2まとめテスト4・解答
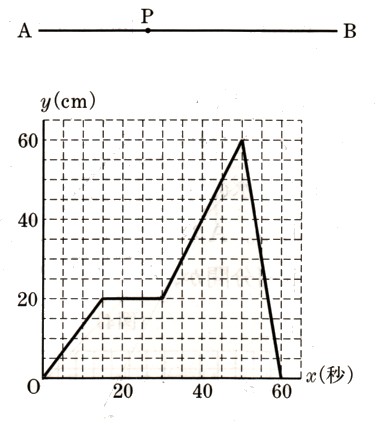
4、 長さ60cmの線分ABがあり、点Pは線分AB上を動くものとします。グラフは、点Pが点Aを出発してから経過した時間をχ秒、点Aからの距離をy?としたときの、χ、yの関係を示したものになります。次の問いに答えて下さい。
長さ60cmの線分ABがあり、点Pは線分AB上を動くものとします。グラフは、点Pが点Aを出発してから経過した時間をχ秒、点Aからの距離をy?としたときの、χ、yの関係を示したものになります。次の問いに答えて下さい。
(1)0≦χ≦60 において、点Pが止まっている時間は何秒間になりますか? 求めて下さい。
止まっている時間は、進んでないということになりますから、グラフでは、水平の部分になります。
グラフの1目盛りは、5秒になりますから、
0~60(秒)の間で水平部分は、(χ、y)=(15,20)~(30,20)になります。
30−15=15(秒)
答え 15(秒)
(2)30≦χ≦50 のとき、yをχの式で表して下さい。
y=aχ+b の式で表すと、
(傾き)は、
(yの増加量) 8
――――――=――=2
(χの増加量) 4
(切片)を求めるために、 y=2χ+b の式に座標(30,20)を代入します。
20=2×30+b
20=60+b
b=20−60
b=−40
(切片)−40になります。
答え y=2χ−40
(3)点Qは、点Pと同時に出発し、線分AB上を点Bに向かって動き、点Bに着いた後は点Bに止まっているものとします。
? 点Qが、点Aから出発し、毎秒a?の速さで動くとき、15<χ<60 において、点Pと点Qが3回重なるようなaの範囲を求めて下さい。
点Qが出発してからχ秒後の点Aからの距離をy?とすると
(距離)=(速さ)×(時間)
y(?)=a × χ
になります。
この直線は、点Pと同時に出発するのですから、原点からになります。
座標でいえば、(30,20)、(50,60)の範囲となります。
20=30a 60=50a
30a=20 50a=60
a=2/3 a=6/5
になり、aの範囲は
2/3<a<6/5
になります。
答え 2/3<a<6/5
? 点Qが、AQ=b? の位置から出発し、毎秒2/5cmの速さで動くとき、50<χ<60で、点Qが点Pと出会うのは、出発してから何秒後になりますか? bの式で表して下さい。ただし、b<40とします。
まずは、点Qをyの式で表します。
(距離)=(速さ)×(時間)+(AQ=b)
y=2/5(?)×χ+b
になります。
点Pと出会いということは、点Pと点Qの交点の座標yが出会う時間になります。
 点Pの 50<χ<60 の直線の式は、グラフのピンクの部分になります。
点Pの 50<χ<60 の直線の式は、グラフのピンクの部分になります。
(傾き)は、右下がりの直線になりますから、符号は(−)になります。
(yの増加量) 6
――――――=−――=−6
(χの増加量) 1
(切片)は、 y=−6χ+b の式に、(χ、y)=(50,60)を代入します。
60=
60=−300+b
−300+b=60
b=360
y=−6χ+360 が 50<χ<60 の直線の式になります。
y=2/5×χ+b
{
y=−6χ+360
ですから、
2/5×χ+b=−6χ+360
2χ+5b=−30χ+1800
2χ+30χ=−5b+1800
32χ=−5b+1800
χ=−5b/32+1800/32
χ=−5b+1800/ 32
−5b+1800/ 32 秒後に出会うということがわかりました。
答え −5b+1800/ 32 秒後











コメント