中学2年数学 図形の調べ方 図形と証明 練習問題4・解答
4、合同の利用
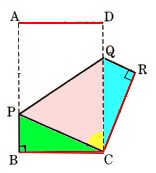
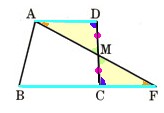
AD//BCである台形ABCDにおいて、辺CDの中点をMとし、AMの延長とBCの延長との交点をFとします。
このとき、△AMD≡△FMCを示すことによって、AM=FMを証明してください。
答え 

〔証明〕
△AMDと△FMCにおいて、
仮定より
CM=DM・・・①
AD//BF
錯角により
∠DAM=∠CFM・・・②
同位角により
∠CMF=∠DMA・・・③
①,②,③より
1つの辺と隣り合う2つの角がそれぞれ等しい。
よって、
△AMD≡△FMC
になります。
ゆえに、合同な三角形の対応する辺の長さは等しくなりますから、
AM=FM
となります。













コメント