中学2年数学 図形の調べ方 まとめテスト4・解答
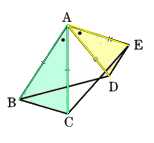
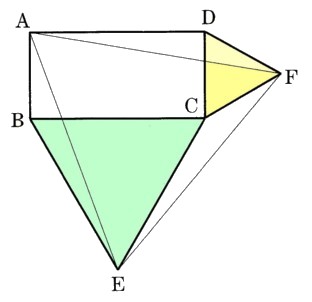
4、図 のように、長方形ABCDの外側に、辺BC、CDを1辺とする正三角形BEC、CFDをつくります。このとき、△AEFは正三角形であることを証明してください。
のように、長方形ABCDの外側に、辺BC、CDを1辺とする正三角形BEC、CFDをつくります。このとき、△AEFは正三角形であることを証明してください。
 のように、長方形ABCDの外側に、辺BC、CDを1辺とする正三角形BEC、CFDをつくります。このとき、△AEFは正三角形であることを証明してください。
のように、長方形ABCDの外側に、辺BC、CDを1辺とする正三角形BEC、CFDをつくります。このとき、△AEFは正三角形であることを証明してください。 答え
〔証明〕

△ADFと△ABEと△CFEにおいて、
仮定により
長方形ABCDで△CFD、△BCEは正三角形ですから
∠ADF=∠ADC+∠CDF=90°+60°
=150°
∠ABE=∠ABC+∠CBE=90°+60°
=150°
∠FCE=360°ー(∠DCB+∠DCF+∠BCE)
=360°ー(90°+60°+60°)
=150°
よって、
∠ADF=∠ABE=∠FCE・・・①
長方形ABCDですから、
辺AB=辺DF
△CDFは、正三角形ですから、
辺DF=辺CF
よって、
辺AB=辺DF=辺CF・・・②
長方形ABCDですから、
辺BC=辺AD
△EBCは、正三角形ですから
辺BE=辺CE
よって、
辺BC=辺AD=辺CE・・・③
①、②、③より
2つの辺とその間の角が、それぞれ等しくなりますから、
△ADF≡△ABE≡△CFE
になります。
合同な三角形の対応する辺は、それぞれ等しくなりますから
△AEFは、正三角形になります。









コメント