中学2年数学 平面図形 平行線と面積 確認問題7・解答
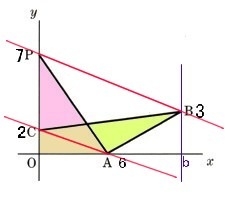
7、図のように、4点O(0,0)、A(6,0)、B(b,3)、C(0,2)、を頂点とする四角形OABCがあり、P(0,7)とします。
四角形OABCの面積と△OAPの面積が等しいとき、bの値を求めてください。

まずは、点Cと点Aをつなぐ直線をかきます。そうすると、底辺が共通な三角形CAPと三角形CABができます。
△CAPと△CABは面積が同じになりますから、平行線の性質から底辺CAが共通で面積が等しければCA//PBになります。
このことにより、線分CAの傾きがわかれば平行な線分PBの傾きもわかります。
(平行な直線は傾きが同じになります。)
それでは考えていきましょう。
式はy=の形で考えます。
y=aχ+b
y=(傾き)χ+(切片)
(切片)は2とわかっていますから、傾きを考えます。

傾きは、右下がりですから符号は(ー)になります。
傾き=yの増加量/χの増加量= 0−2/6−0
=−1/3
になります。
それでは,式に代入していきます。
y=ーχ/3+2 になります。
つぎに、線分PBの式を考えます。
傾きが同じで,(切片)が7ですから、
y=−χ/3+7
になります。
この式にわかっている点Bのy=3を代入します。
3=−χ/3+7
−χ/3+7=3
−χ/3=3−7
−χ/3=−4
−χ=−12
χ=12
答え b=12





コメント