中学2年数学 確率 2まとめテスト7・解答
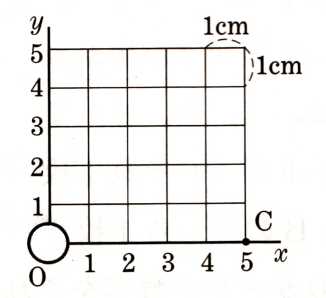
7、図 のように,1目盛りが1㎝の座標平面上の点O(0、0)におはじきがあります。
のように,1目盛りが1㎝の座標平面上の点O(0、0)におはじきがあります。
 のように,1目盛りが1㎝の座標平面上の点O(0、0)におはじきがあります。
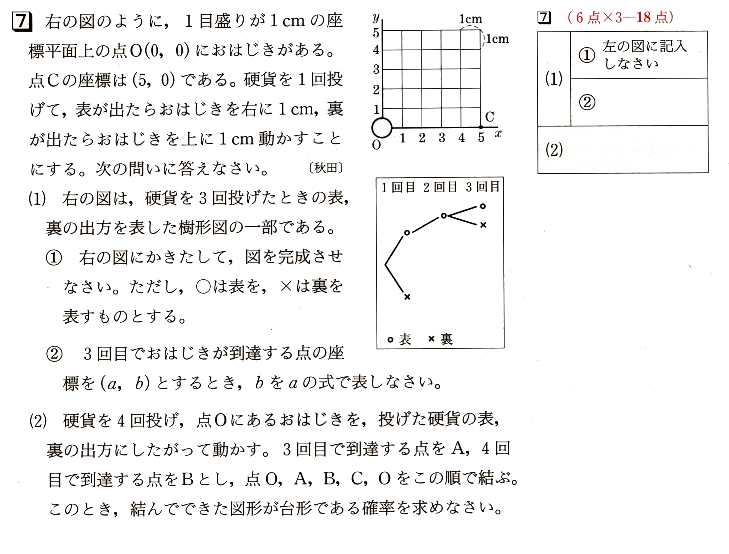
のように,1目盛りが1㎝の座標平面上の点O(0、0)におはじきがあります。 点Cの座標は,(5、0)であるとき、硬貨を1回投げて表が出たらおはじきを右に1㎝、
裏が出たらおはじきを上に1㎝動かすこととします。次の問いに答えてください。
(1)図 は硬貨を3回投げたときの表、裏の出方を表した樹形図の一部になります。
は硬貨を3回投げたときの表、裏の出方を表した樹形図の一部になります。
 は硬貨を3回投げたときの表、裏の出方を表した樹形図の一部になります。
は硬貨を3回投げたときの表、裏の出方を表した樹形図の一部になります。 ① 図にかき足して,図を完成させてください。ただし,○は表,×は裏を表すものとします。
答え 

② 3回目でおはじきが到達する点の座標を(a,b)とするとき、bをaの式で表してください。
図 を見てください。
を見てください。
 を見てください。
を見てください。 上から①、②,③、④,⑤、⑥,⑦、⑧とします。
①右→右→右 3㎝右に移動 (3、0)
②右→右→上 2㎝右1㎝上に移動(2、1)
③右→上→右 2㎝右1㎝上に移動(2、1)
④右→上→上 1㎝右2㎝上に移動(1、2)
⑤上→右→右 2㎝右1㎝上に移動(2、1)
⑥上→右→上 1㎝右2㎝上に移動(1、2)
⑦上→上→右 1㎝右2㎝上に移動(1、2)
⑧上→上→上 3㎝上に移動 (0、3)
表を見ると、a+b=3となっています。
bをaの式で表すのですから、
b=3ーa
になります。
答え b=3ーa
(2)硬貨を4回投げて,点Oにあるおはじきを,投げた硬貨の表,裏の出方に従って動かします。
3回目で到達する点をA、4回目で到達する点をBとし、点O、A、B,C,Oをこの順で結びます。
このとき、結んでできた図形が台形である確率を求めてください。
台形になる場合を考えていきます。
台形は、上底と下底が平行な四角形になります。
図 を見てください。
を見てください。
 を見てください。
を見てください。 3回目の位置と4回目の位置が次のときに台形になることがわかります。

A(0、3)、B(1、3)
A(1、2)、B(2、2)
A(2、1)、B(3、1)
になります。
この条件を満たしている座標を表から選んでください。
A(0、3)、B(1、3)1通り
A(1、2)、B(2、2)3通り
A(2、1)、B(3、1)3通り
合計7通りになります。
(台形になる確率)=(台形になる場合の数)÷(全部の場合の数)
=7/16
答え 7/16








コメント