中学3年数学 y=aχ²の値の変化 2確認問題2・解答
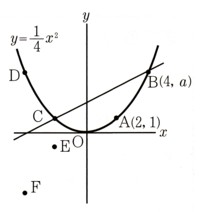
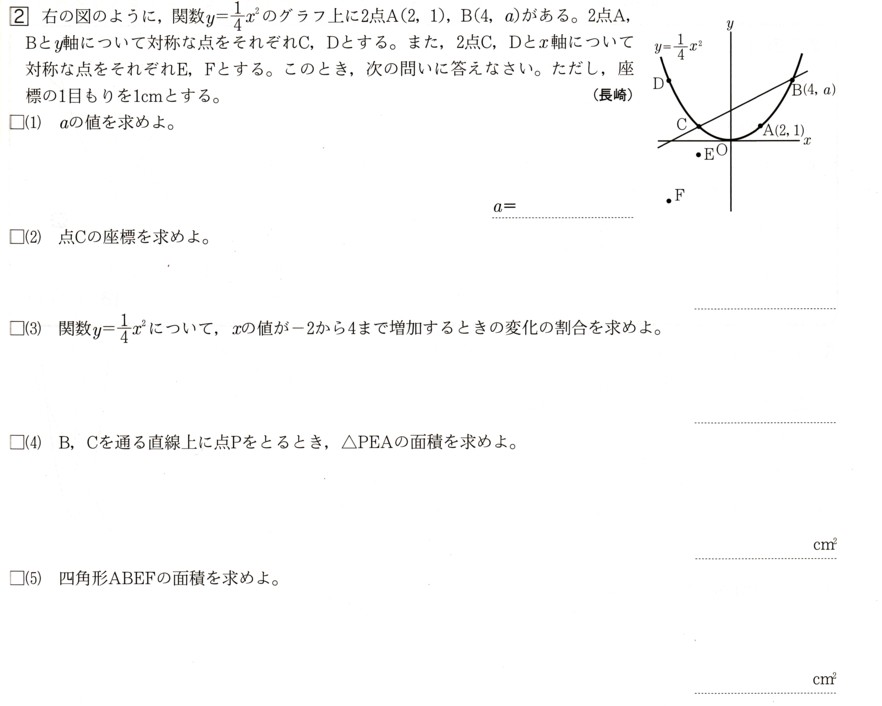
2、図 のように、関数y=1/4χ²のグラフ上に2点A(2,1)、B(4、a)があります。2点A,Bとy軸について対称な点を
のように、関数y=1/4χ²のグラフ上に2点A(2,1)、B(4、a)があります。2点A,Bとy軸について対称な点を
それぞれC,Dとします。また、2点C,Dとχ軸について対称な点をそれぞれE,Fとします。このとき、次の問いに答えてください。
ただし、座標の1目盛りを1cmとします。
(1)aの値を求めてください。
まずは、y=1/4χ²にA(2,1)、B(4、a)を代入します。
a=1/4×4²
a=16/4
a=4
答え a=4
(2)点C,の座標を求めてください。
点Cのy座標はy軸に対象ですから点Aのy座標と同じですから1になり、
点Aのχ座標と符号が変わり−2になります。
答え Cの座標(χ、y)=(−2,1)
(3)関数y=1/4χ²について、χの値がー2から4まで増加するときの変化の割合を求めてください。
y=1/4χ² にχ=−2、χ=4を代入します。
y=1/4×(−2)² 、y=1/4×4²
y=1/4×4 、y=1/4×16
y=1 、y=4
yは1から4まで増加しました。
yの増加量
変化の割合=―――――――
χの増加量
4−1 3 1
―――――=――=―
4−(−2) 6 2
1
答え 変化の割合=――
2
(4)B,Cを通る直線上に点Pをとるとき、△PEAの面積を求めてください。

仮説ををたててみましょう。
直線CBと直線AEが平行ならば底辺をAEと考えたとき高さはすべて同じになるので同じ面積になるということがわかります。
そのために、直線CBの傾きと直線AEの傾きが同じなら2つの直線は平行だということがわかります。
まずは直線CBの式を考えます。
直線ですからy=aχ+b の式になります。
(3)で傾きはわかっていますから、点Cの座標(−2,1)を代入してみましょう。
1=1/2×(−2)+b
1=−1+b
b=1+1
b=2
直線CBの式はy=1/2χ+2
次に、直線AEの式を考えます。
点A(2,1)点Eの座標は点Cとχ軸上に対象ですから(−2、−1)になります。
y=aχ+b の式2つの座標をあてはめてみます。
1=2a+b
{
−1=−2a+b
(加減法)
1=2a+b
−)−1=−2a+b
2=4a
a=1/2
1=2a+bにa=1/2を代入します。
1=2×1/2+b
1=1+b
b=0
切片は0ですから原点になり、
式は
y=1/2χ
となり、直線CB(y=1/2χ+2)と傾きが同じですから、2つの直線








コメント