中学3年数学 図形と相似(そうじ)
1、相似(そうじ)な図形
○拡大・縮小
ある図形を、その形を変えないで、一定の割合で大きくすることを「拡大」。
小さくすることを「縮小」。
といいます。
○相似(そうじ)
2つの図形があって、一方の図形を拡大または縮小したものと、他方の図形が合同であるとき、
この2つの図形は相似(そうじ)であるといいます。
○相似(そうじ)な図形の性質
?対応する辺の長さの比が、すべて等しい。
?対応する角の大きさが、それぞれ等しい。
○相似な多角形と相似比

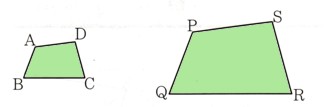
●四角形ABCDと四角形PQRSが相似であるとき、相似の記号∽(そうじ)を使って、
四角形ABCD∽四角形PQRS
と書きます。このとき、対応する頂点を順に並べます。
●相似な2つの多角形で、対応する辺の長さの比を相似比(そうじひ)といいます。
例:
図で、△ABCと△DEFが相似であるとき、AB:DE=1:2ですから、
相似比は1:2となります。
○線分の比と相似比
●比a:bは、2つの数量a、bを比べたもので、aをbで割った値a/bをa:bの比の値といいます。
●等しい比 a:bの比の値a/bとc:dの比の値c/dが等しいとき、2つの比a:bとc:dは等しいといいます。
a:b=c:d と表します。
●a:b=c:dならば ad=bc が成り立ちます。
2、三角形の相似条件
○2つの三角形は、次のどれか1つを満たすとき相似であるといいます。
?3組の辺の比が、すべて等しいとき。
?2組の辺の比とその間の角が、それぞれ等しいとき。
?2組の角がそれぞれ等しいとき。
3、相似条件と証明
○三角形の相似条件も証明の根拠として使うことができます。
4、縮図の利用
直接には測ることのできない2地点間の距離や建物の高さなどを、縮図をかいて求める方法があります。






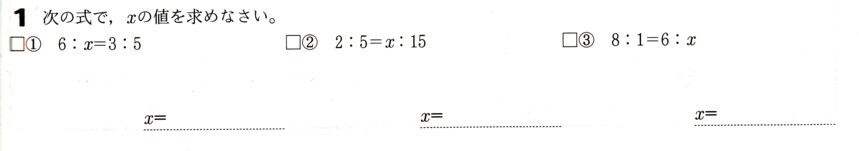
コメント