中学3年数学 三平方の定理の利用 4確認問題3・解答
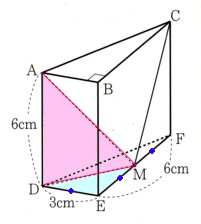
3、次の図 のような、AD=EF=6cm、DE=3cm、∠ABC=90゜の三角柱ABCDEFがあります。
のような、AD=EF=6cm、DE=3cm、∠ABC=90゜の三角柱ABCDEFがあります。
いま、辺EFの中点をMとし、点Mと点A,点Mと点C,点Mと点Dをそれぞれ結びます。
このとき出来る四角錘MADFCを考えるとき、次の問いに答えてください。
(1)MAの長さを求めてください。
△ADMで考えます。
そのためには、△MDEの斜辺を求めなければいけません。
底辺をDE=3?
高さをEM=FE(6cm)の中点=3?
斜辺をDM=χで三平方の定理を使い考えます。
(底辺)²+(高さ)²=(斜辺)²
3²+3²=χ²
9+9=χ²
18=χ²
χ=√18(χは+になります)
χ=3√2?
DM=3√2?・・・?
これで、△ADMの底辺=DMの長さが3√2とわかりました。
高さ=AD=6cm
斜辺=AM=χとして三平方の定理を使い考えます。
(底辺)²+(高さ)²=(斜辺)²
(3√2)²+6²=χ²
18+36=χ²
54=χ²
χ=√54(χは+になります)
χ=3√6cm
AM=3√6?
答え 3√6?
(2)四角錘MADFCの体積を求めてください。
点Mを頂点に点ADFCを底面とした四角錘で考えます。
四角錘の面積は(底面積)×(高さ)×1/3
(底面積)
AD×DF
AD=6cm
DF=AC
△DFEを三平方の定理によりわかります。

△DFEの辺DE、辺FEの長さを1つずつ考えます。
辺DEは△DFEの底辺の長さになります。
斜辺=FD=χ?
底辺=DE=3?
高さ=FE=6cm
(底辺)²+(高さ)²=(斜辺)²
(3)²+(6)²=(χ)²
9+36=χ²
45=χ²
χ=√45=FD=3√5?
これで、底面積がわかりました。
6×3√5=18√5㎠・・・?
次に高さを考えます。高さは点Mを頂点に考えますから












コメント