中学3年数学 三平方の定理の利用 練習問題7(2)・解答
7、次の問いに答えてください。
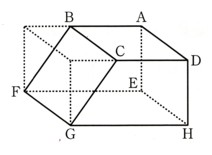
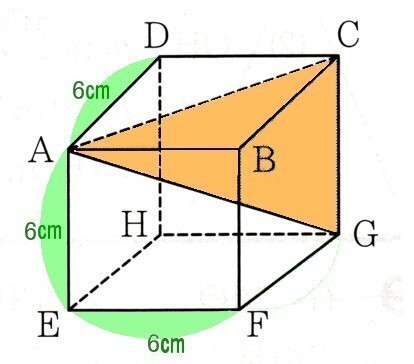
(2)1辺6?の立方体の対角線の長さを求めてください。

△ABCで考えます。
∠ABC=90゜
ですから、直角三角形ということがわかります。
底辺をAB=6?
高さをBC=6?
斜辺をAC=χ?として三平方の定理を利用して考えます。
(底辺)²+(高さ)²=(斜辺)²
(6)²+(6)²=(χ)²
36+36=χ²
72=χ²
χ=√72(χは+になります)
3)72
3)24
2) 8
2) 4
2
χ=6√2?
AC=6√2?

次に△ACGで考えます。
∠ACG=90゜
底辺をCG=6?
高さをAC=6√2?・・・?より
斜辺をAG=χ?として三平方の定理を利用し考えます。
(底辺)²+(高さ)²=(斜辺)²
(6)²+(6√2)²=(χ)²
36+72=χ²
108=χ²
χ=√108(χは+ですから)
3)108
3) 36
2) 12
2) 6
3
χ=6√3?
AG=6√3?
答え 6√3?
立方体の対角線を求める式は
ℓ=√a²+b²+c²
(立方体の対角線)=√(縦)²+(横)²+(高さ)²
縦6?、横6?、高さ6? ですから、
√(6)²+(6)²+(6)²
=√36+36+36
=√108
=6√3





コメント