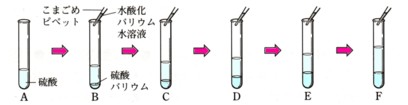
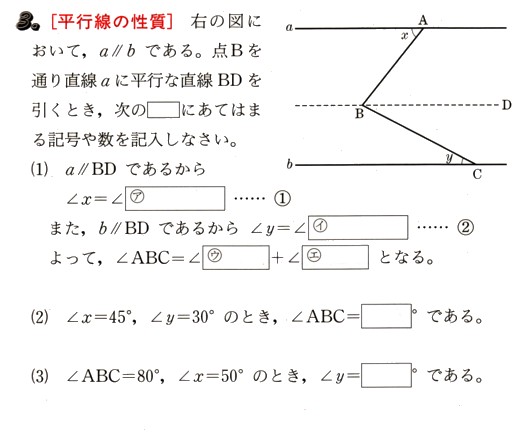
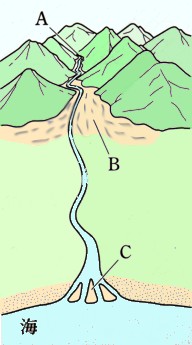
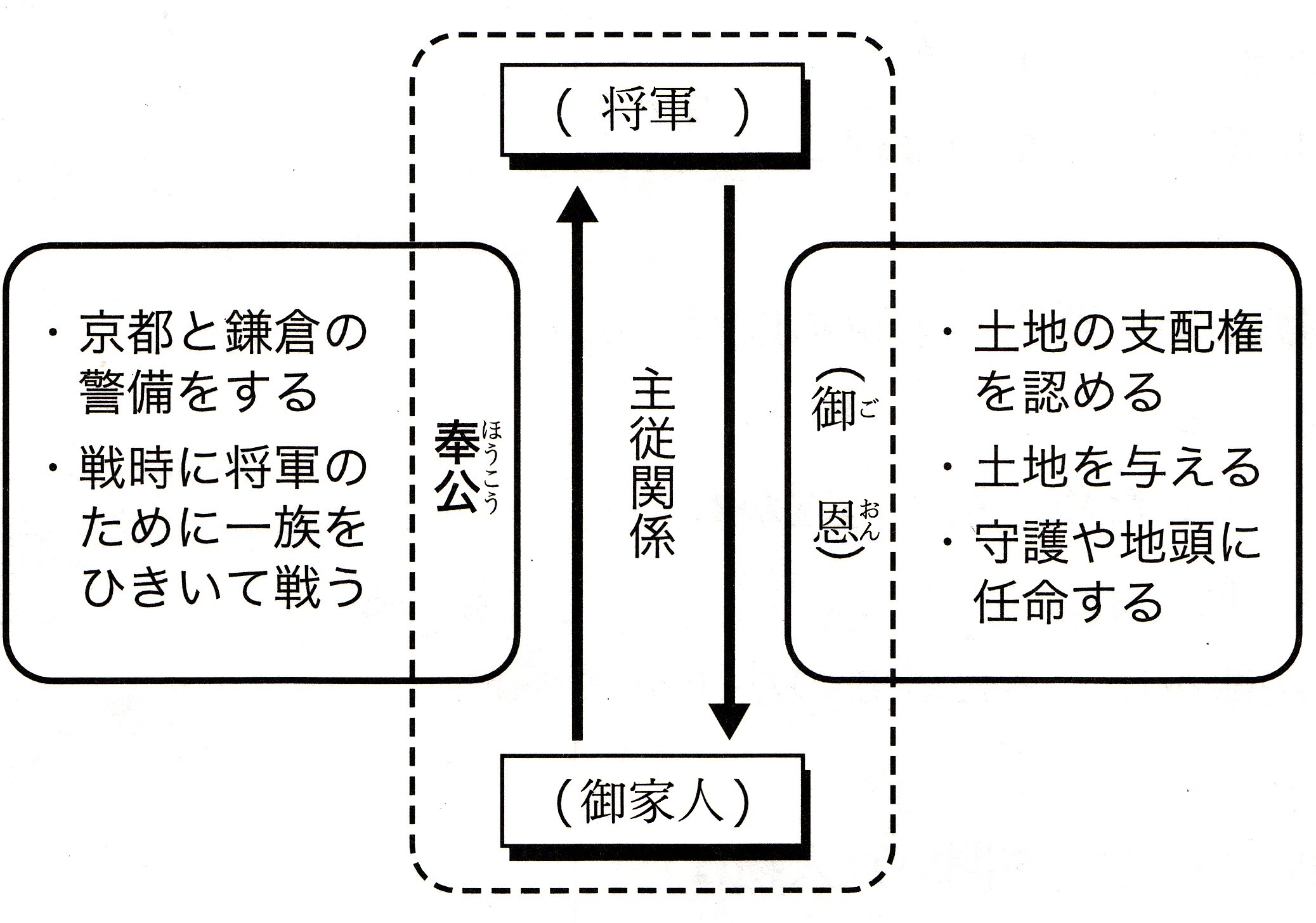
中学３年数学　三平方の定理の利用　４確認問題4・解答

（１）

CA は△ADCの斜辺になります。

△ADCの斜辺を、三平方の定理を利用して求めます。

底辺＝AD＝4cm

高さ＝CD＝8cm

斜辺＝CA＝x²

（斜辺）²＝（底辺）²＋（高さ）²

$\displaystyle x^{2}=4^{2}+8^{2}$ $\displaystyle x^{2}=16+64$ $\displaystyle x^{2}=80$ $\displaystyle x=\sqrt{80}\,(x\geq0)$

$\displaystyle \sqrt{80}$ は以下のように素因数分解します。
$\displaystyle 2)\underline{80}\\2)\underline{40}\\2)\underline{20}\\2)\underline{10}\\~~~~~5$

$\displaystyle x=\sqrt{2\times2\times2\times2\times5}$ $\displaystyle x=\sqrt{4\times4\times5}$

$\displaystyle x=4\sqrt{5}$

AC＝斜辺＝ $\displaystyle 4\sqrt{5}$

AC:AP＝8:3

線分APの長さをxとして求めます。線分ACの長さは $\displaystyle 4\sqrt{5}$ と求められていますから、以下のようになります。

$\displaystyle 4\sqrt{5}\times3=AP\times8$ $\displaystyle 12\sqrt{5}=8AP$ $\displaystyle AP=\frac{12\sqrt{5}}{8}$ $\displaystyle AP=\frac{3\sqrt{5}}{2}$

答え　 $\displaystyle \frac{3\sqrt{5}}{2}$ cm

（２）

この図形で考えるのは高さを求めることになります。

高さはCGの長さがわかれば求めることができます。

△PAQと△PGCで考えます。

直線AC上に∠GPQ＝90゜がありますから、

180゜−（∠CPG＋∠GPQ）＝∠APQ

三角の内角の和は180゜ですから、

180゜-（∠CPG＋∠PCG）＝∠CGP

よって、

∠APQ＝∠CGP・・・①

∠PAQ＝∠PCG＝９０゜・・・②

①，②より

２組の角がそれぞれ等しくなりますから

△PAQ∽△PGC

∴　AQ：PC＝AP：CG

CGをxとして考えます。

そうすると、CG＝AE

AE:AQ＝３：１になりますから、

AQはAEの $\displaystyle \frac{1}{3}$ になります。

ですから、AQ＝ $\displaystyle \frac{x}{3}$

PC＝AC+APですから、

AC＝ $\displaystyle 4\sqrt{5}$ ・・・（１）より

AP＝ $\displaystyle \frac{3\sqrt{5}}{2}$ ・・・（１）より

PC＝ $\displaystyle 4\sqrt{5}-\frac{3\sqrt{5}}{2}$

＝ $\displaystyle \frac{8\sqrt{5}}{2}-\frac{3\sqrt{5}}{2}$

＝ $\displaystyle \frac{5\sqrt{5}}{2}$

$\displaystyle \frac{x}{3}:\frac{5\sqrt{5}}{2}=\frac{3\sqrt{5}}{2}:x$ $\displaystyle \frac{x}{3}\times x=\frac{5\sqrt{5}}{2}\times\frac{3\sqrt{5}}{2}$ $\displaystyle \frac{x^{2}}{3}=\frac{75}{4}$ $\displaystyle x^{2}=\frac{75\times3}{4}$ $\displaystyle x^{2}=\frac{225}{4}$ $\displaystyle x=\frac{\sqrt{225}}{2}(x\geq0)$

$\displaystyle \sqrt{225}$ は以下のように素因数分解します。
$\displaystyle 3)\underline{225}\\3)\underline{~75}\\5)\underline{~25}\\~~~~~~5$