中学2年数学 図形の調べ方 まとめテスト6・解答
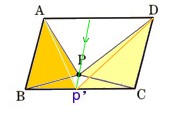
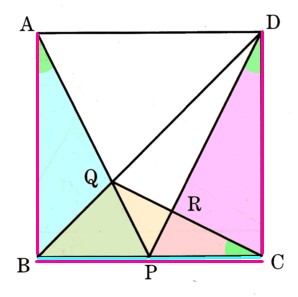
6、正方形ABCDの辺BCの中点をPとします。また、対角線とAPとの交点をQ、QCとDPの交点をRとするとき、次の問いに答えてください。
(1)∠BAPと等しい角をすべて答えてください。

△ABPと△DCPにおいて、
仮定より、
□ABCDは、正方形ですから、
AB=CD・・・?
∠ABP=∠DCP・・・?
BP=CP・・・?
?、?、?より
2つの辺とその間の角が、それぞれ等しくなりますから。
△ABP≡△DCP
合同な三角形の対応する角は等しくなりますから、
∠BAP=∠CDP
になります。
つぎに、

△ABQと△CBQにおいて、
仮定より、
□ABCDは正方形ですから、
AB=BC・・・?
BDは対角線ですから、∠Bの二等分線になりますから。
∠ABQ=∠CBQ・・・?
BQは、共通な辺になります。・・・?
?、?、?により
2つの辺とその間の角がそれぞれ等しくなりますから、
△ABQ≡△CBQ
合同な三角形の対応する角はそれぞれ等しくなりますから
∠BAQ=∠BCQ
になります。
答え ∠CDP、∠BCQ
(2)(1)を用いて、DP⊥QCであることを証明してください。
(1)より、

△ABPにおいて
∠BAP+∠APB+∠ABP=180°
∠BAP=∠QCB・・・?
∠APB=∠DPC・・・?
次に、△RCPについて、

∠QCB+∠DPC+∠CRP=180°
∠ABP=90°ですから、
∠BAP+∠APB+90°=∠QCB+∠DPC+∠CRP
90°=∠CRP
2つの直線が90°に交わる場合は、2つの直線は垂直に交わりますから、
DP⊥QC
になります。







コメント