中学2年数学 平面図形 2まとめテスト1・解答
1、三角形ABCにおいて、∠BAC=120°であるとき、(1)、(2)の場合について∠ABCの大きさを求めてください。ただし、図は正確ではありません。
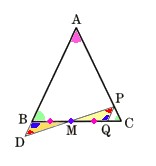
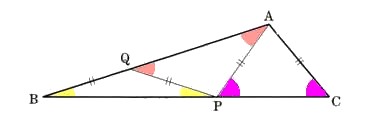
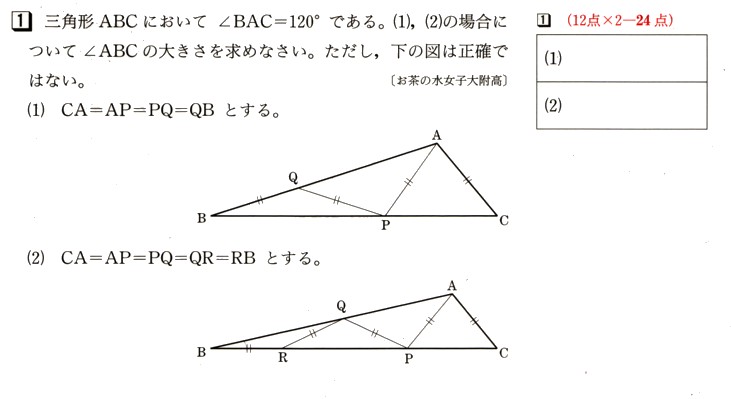
(1)CA=AP=PQ=QBとします。

△BQP、△PQA、△APCの3つの三角形は2つの辺がそれぞれ等しくなりますから,
二等辺三角形ということがわかります。
∠Bをχ°として考えていきます。
仮定より∠BAC=120°ですから
∠Cは、三角形の内角の和(180°)から2つの角の和を引いた角度になります。
∠B=χですから
∠BAC=120°
∠BCA=180°ー(120°+χ)
∠QPBは二等辺三角形BQPの底角になりますから
∠QPB=χ°
∠PQAは、△BQPの外角になりますから、
∠QPB=2χ°
∠QAPは、二等辺三角形PQAの1つの底角になりますから
∠QAP=2χ°
つぎに、∠APCについて考えます。
△ABPの2つの角、∠ABPと∠BAPの2つの角の和が外角(∠APC)になります。
∠APC=∠ABP+∠BAP
=χ°+2χ°
=3χ°
∠ACPは、△APC(二等辺三角形)の1つの底角になります。
∠ACP=3χ°

∠PACは,三角形の内角の和から
∠PAC=180°ー(3χ°+3χ°)
=180°ー6χ°
∠BACは、120°。
∠BAC=120°
∠BAC=∠QAP+∠PAC
120°=2χ°+(180°ー6χ°)
120°=2χ°+180°ー6χ°
2χ°ー6χ°=120°ー180°
−4χ°=ー60°
χ=15°
答え ∠ABC=15°
(2) CA=AP=PQ=QR=RBとします。
CA=AP=PQ=QR=RBとします。
今回は,∠ABCをyとして考えます。
∠BAC=120°
(1)と同じように考えていきます。
△BRQは二等辺三角形になります。
∠QBR=y°
∠BQR=y°
△QRPについて考えます。
∠QRPは、△BQRの外角になりますから、
∠QRP=2y°
△QRPは二等辺三角形ですから
∠QPR=2y°
 次に∠AQPについて考えます。
次に∠AQPについて考えます。
∠AQPは、△QBPの∠QBPと∠QPBの外角になります。
∠AQP=∠QBP+∠QPB
∠AQP=y°+2y°
∠AQP=3y°
△AQPは二等辺三角形ですから、
∠QAP=3y°
 つぎに、∠APCについて考えます。
つぎに、∠APCについて考えます。
∠APCは△ABPの∠ABPと∠BAPの外角になります。
∠APC=∠ABP+∠BAP
∠APC=y°+3y°
∠APC=4y°
△APCは二等辺三角形になりますから
∠ACP=4y°になります。
 △ABCについて考えます。
△ABCについて考えます。
三角形の内角の和は180°になりますから
∠ABC=y°
∠ACB=4y°
∠BAC=120°
(三角形の内角の和)=∠ABC+∠ACB+∠BAC
180°=y°+4y°+120°
y°+4y°=180°ー120°
5y°=60°
y=12°
答え ∠ABC=12°






コメント