中学２年数学　平面図形　２まとめテスト4・解答

中学２年数学　平面図形　２まとめテスト4・解答

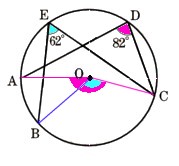
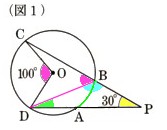
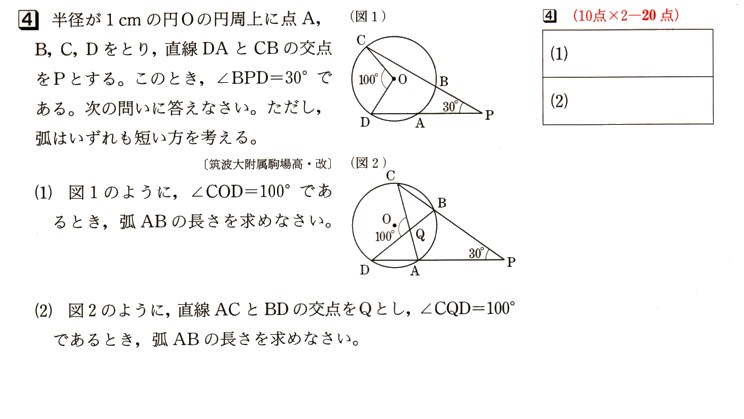
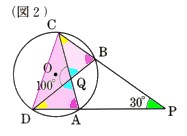
４、半径が１?の円Ｏの円周上に点Ａ、Ｂ、Ｃ、Ｄをとります。直線ＤＡとＣＢの交点をＰとします。このとき、∠ＢＰＤ＝30°になります。

　　次の問いに答えてください。ただし、弧はいずれも短い方を考えてください。

（１）図１のように、∠ＣＯＤ＝100°であるとき、弧ＡＢの長さを求めてください。

　　　∠ＣＯＤ＝100°ですから

　　　弧ＣＤの中心角になります。

　　　∠ＣＢＤは弧ＣＤの円周角になります。

　　　同じ弧の円周角は中心角の半分になりますから。

　　　∠ＣＢＤ＝∠ＣＯＤ÷２

　　　　　　　＝100°÷2

　　　　　　　＝50°

　　　∠ＣＢＤ＝50°・・・?

　　　次に、△ＢＤＰについて考えます。

　　　∠ＢＰＡ＝30°・・・?

　　　∠ＰＢＤは、直線から∠ＣＢＤを引いた角度になります。

　　　∠ＰＢＤ＝180°−50°

　　　∠ＰＢＤ＝130°・・・?

　　　次に、∠ＢＤＰについて考えます。
　　
　　三角形の内角の和は180°になりますから

　　∠ＢＤＰ＝180°ー(∠ＤＢＰ＋∠ＢＰＤ)

　　　　　　＝180°ー(130＋30)

　　　　　　＝180°ー160°

　　　　　　＝20°

 

　　これで、弧ＡＢの円周角が20°とわかりました。

　　同じ弧の中心角は円周角の2倍になりますから。

　　弧ＡＢの円周角×２＝弧ＡＢの中心角

　　∠ＢＤＡ×２＝∠ＢＯＡ

　　20°×2＝40°

　　∠ＢＯＡ＝40°

　　弧ＡＢの中心角が40°とわかりました。

　　ここから長さになります。

　　この円の円周の40°／360°が弧ＡＢの長さになります。

　　この円の円周は

　　半径が1cmですから、半径×2×π　になりますから、

　　1×2×π＝2π(?)

　　円周(２π?)の40／360＝1／9

　　弧ABの長さ＝(円周の長さ)×1／9

　　　　　　　＝2π?×1／9

　　　　　　　＝2π／9(?)

 

　　答え　2／9　π　（?）