中学3年数学 式の展開と因数分解 因数分解 練習問題9・解答
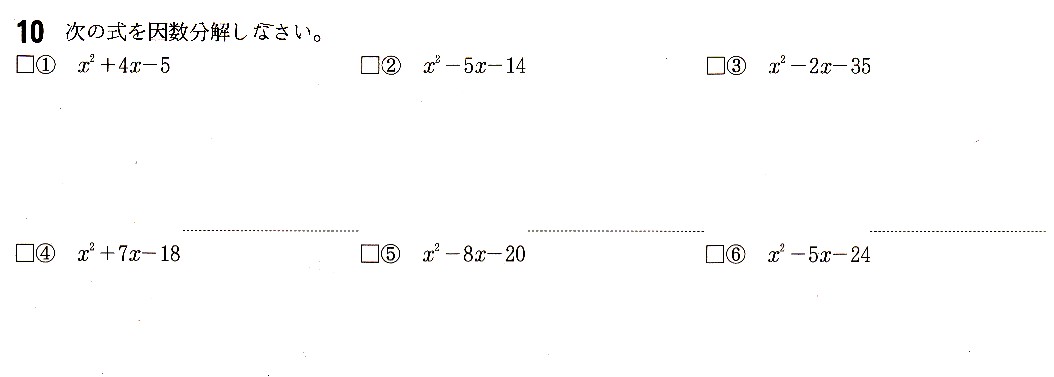
9、次の式を因数分解してください。
乗法公式を利用して因数分解をします。
今回の式の場合は、χ²+(a+b)χ+ab=(χ+a)(χ+b)
を利用します。
①,χ²+4χ+3
かけて、3 (1×3、3×1)
たして、4 (1+3、2+2、3+1)
の共通する数を探します。
1、3になります。
χ²+4χ+3=(χ+1)(χ+3)
答え (χ+1)(χ+3)
②,χ²−8χ+15
かけて15 (1×15、3×5、5×3、15×1、ー1×ー15、ー3×ー5、ー5×ー3、ー15×ー1)
たして−8 上の数の組み合わせの中で−8になるのは、「(−3)+(−5)、(−5)+(−3)」
になり共通する数は(−3)、(−5)になります。
χ²−8χ+15=(χ−3)(χ−5)
答え (χ−3)(χ−5)
③,χ²+12χ+20
かけて20 (1×20、2×10、4×5、5×4、10×2、20×1)
たして12 (2+10、10+2)
2、10が共通な数になります。
χ²+12χ+20=(χ+2)(χ+10)
答え (χ+2)(χ+10)
④,a²−13a+30
かけて30 (1×30、2×15、3×10、5×6、6×5、10×3、15×2、30×1、ー1×ー30、ー2×ー15、ー3×ー10、ー5×ー6、ー6×ー5、ー10×ー3、ー15×ー2、ー30×ー1)
たしてー13 「−3+(−10)、−10+(ー3)」
共通な数は(−3)、(−10)になります。
a²−13a+30=(a−3)(a−10)
答え (a−3)(a−10)
⑤,y²+20y+36
かけて36 (1×36、2×18、3×12、4×9、6×6、9×4、12×3、18×2、36×1)
たして20 (2+18、18+2)
(+2)(+18)が共通な数になります。
y²+20y+36=(y+2)(y+18)
答え (y+2)(y+18)
⑥,b²+14b+40
かけて40 (1×40、2×20、4×10、5×8、8×5、10×4、20×2、40×1)
たして14 (4+10、10+4)
(+4)(+10)が共通な数になります。
b²+14b+40=(b+4)(b+10)
答え (b+4)(b+10)








コメント