中学3年数学 二次方程式 2確認問題1・解答
1、次の方程式を解いてください。
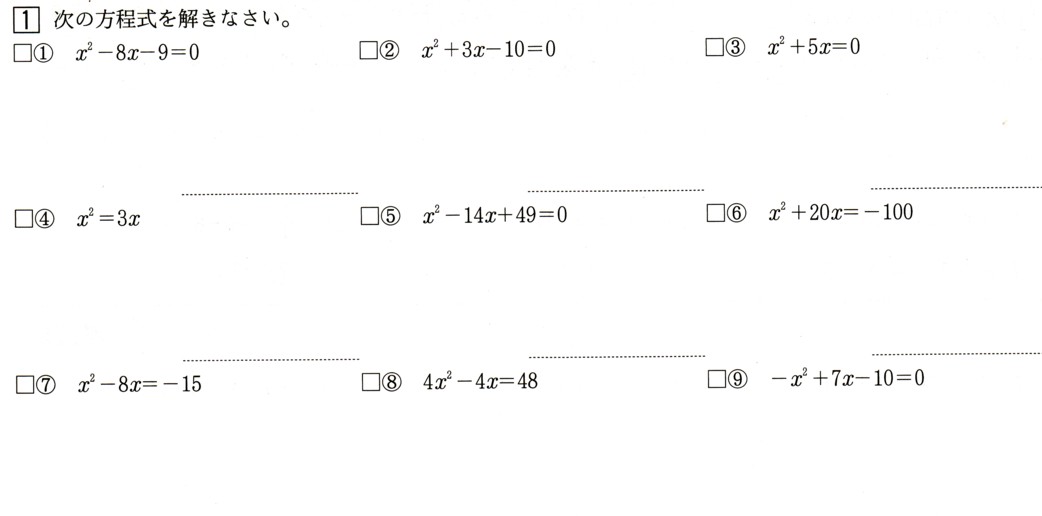
?,χ²ー8χー9=0
因数分解をします。
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー9、足してー8になる2つの数は
ー9×1=−9,ー9+1=−8
χ²ー8χー9=(χー9)(χ+1)
(χー9)(χ+1)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χー9=0
χ=9
χ+1=0
χ=−1
答え χ=9、χ=−1
?,χ²+3χー10=0
因数分解をします。
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー10、足して3になる2つの数は
ー2×5=10、ー2+5=3
χ²+3χー10=(χー2)(χ+5)
(χー2)(χ+5)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
(χー2)=0、(χ+5)=0
χ=2、χ=ー5
答え χ=2、χ=−5
?,χ²+5χ=0
共通因数はχになります。
χ(χ+5)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χ=0
χ+5=0
χ=−5
答え χ=0、χ=−5
?,χ²=3χ
χ²−3χ=0
共通因数はχになります。
χ(χー3)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χ=0
χー3=0
χ=3
答え χ=0、χ=3
?,χ²ー14χ+49=0
因数分解をします。
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけて49、足してー14になる2つの数は
(ー7)×(−7)=49,(ー7)+(−7)=−14
χ²ー14χー49=(χー7)(χ−7)
=(χー7)²
(χー7)²=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χー7=0
χ=7
答え χ=7
?,χ²+20χ=ー100
χ²+20χ+100=0
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけて100、足して20になる2つの数は
10×10=100,10+10=20
χ²ー20χ+100=(χ+10)²
(χ+10)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χ+10=0
χ=−10
答え −10
?,χ²ー8χ=ー15
χ²−8χ+15=0
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけて15、足してー8になる2つの数は
(ー3)×(−5)=15,(ー3)+(−5)=−8
χ²ー8χー9=(χー3)(χ−5)
(χー3)(χー5)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χー3=0
χ=3
χー5=0
χ=5
答え χ=3、χ=5
?,4χ²ー4χ=48
両辺を4で割ります。
χ²ーχ=12
χ²ーχー12=0
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけてー12、足してー1になる2つの数は
ー4×3=−12,ー4+3=−1
χ²ーχー12=(χー4)(χ+3)
(χー4)(χ+3)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χー4=0
χ=4
χ+3=0
χ=−3
答え χ=4、χ=−3
?,ーχ&su
p2;+7χー10=0
両辺にー1をかけます。
χ²ー7χ+10=0
●χ²+χ(a+b)+ab=(χ+a)(χ+b)
かけて10、足してー7になる2つの数は
ー2×(−5)=10,ー2+(−5)=−7
χ²ー7χ+10=(χー2)(χー5)
(χー2)(χー5)=0
A×B=0ならば、 A=0 または B=0 になります。
ですから、
χー2=0
χ=2
χー5=0
χ=5
答え χ=2、χ=5









コメント