中学3年数学 図形と相似 まとめテスト3・解答
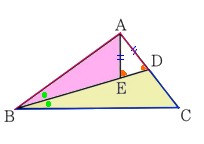
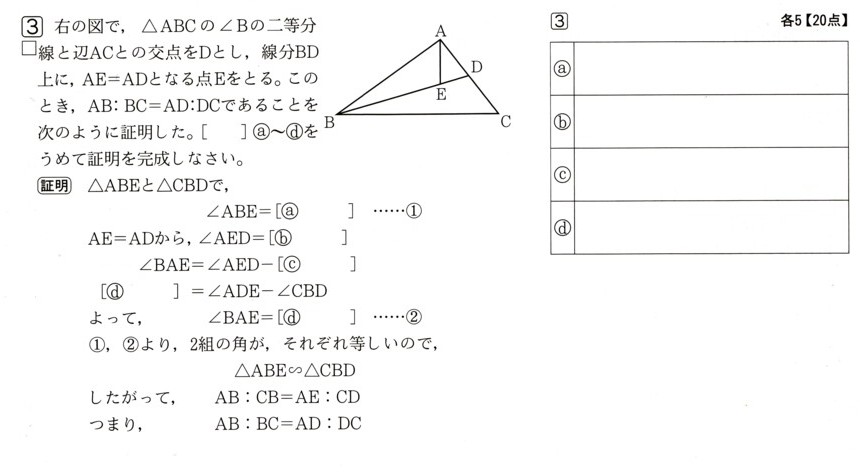
3、次の図 で、△ABCの∠Bの二等分線と辺ACとの交点をDとします、線分BD上に、AE=AD
で、△ABCの∠Bの二等分線と辺ACとの交点をDとします、線分BD上に、AE=AD
となる点Eをとります。このとき、AB:BC=AD:DCであることを次のように証明しました。
[ ]a~dを埋めて証明を完成してください。
〔証明〕
△ABE と△CBDで、
∠ABE =[a ]・・・?
AE=AD から、
∠AED=[b ]
∠BAE=∠AED−[c ]
[d ]=∠ADE−∠CBD
よって、
∠BAE=[d ]・・・?
?,?より、2組の角が、それぞれ等しいので、
△ABE∽△CBD
したがって、
AB:CB=AE:CD
つまり、
AB:BC=AD:DC
答え
〔証明〕
△ABEと△CBDで、
∠ABE=[a∠CBD]・・・?
AE=ADから、
∠AED=[b∠ADE]
∠BAE=∠AED−[c∠ABE]
[d∠BCD]=∠ADE−∠CBD
よって、
∠BAE=[d∠BCD]・・・?
?,?より、2組の角が、それぞれ等しいので、
△ABE∽△CBD
したがって、
AB:CB=AE:CD
つまり、
AB:BC=AD:DC
a∠CBD、b∠ADE、c∠ABE、d∠BCD








コメント