中学3年数学 図形と相似 平行線と線分の比 2確認問題4・解答
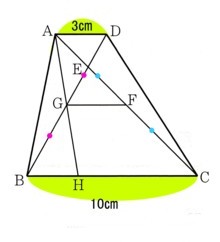
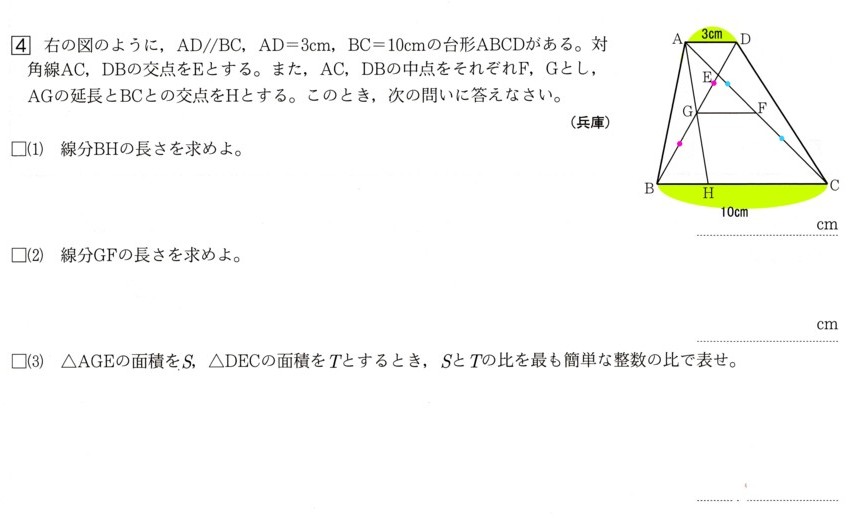
4、次の図 のように、AD//BC、AD=3cm、BC=10cmの台形ABCDがあります。
のように、AD//BC、AD=3cm、BC=10cmの台形ABCDがあります。
対角線AC,DBの交点をEとします。また、AC、DBの中点をそれぞれF,Gとし、
AGの延長とBCとの交点をHとします。このとき、次の問いに答えてください。
(1)線分BHの長さを求めてください。
△AGD と△HGBで考えます。
仮定より AD//BC になります。
これにより、∠DAG=∠BHG(錯覚)・・・?
∠ADG=∠HBG(錯覚)・・・?
GD=GB (仮定より)
よって、△AGD=△HGB
となります。
∴AD=BHですから
AD =3cm
BH =3cm
となります。
答え 3cm
(2)線分GFの長さを求めてください。
△AHC と△AGFで考えます。
△AHC の底辺の長さ HC=(BC–BH)ですから
(10?ー3cm)=7cm=HC
点Gは辺AHの中点 になり、
点Fは辺ACの中点 になりますから、
中点連結定理 を使います。
これにより、GF//HC 、GF=1/2HC となります。
HC=7cm ですから、
GF=1/2×7
=3.5?
答え 3.5?
(3)△AGEの面積をS、△DECの面積をTとするとき、SとTの比を最も簡単な整数の比で表してください。
△AGEと△DECは相似の関係にはないので、相似の関係になる△を探します。
△AED をUとして考えます。
△EG Fと△EDAは
AD//GF ですから、
∠ADE=∠FGE(錯覚)・・・?
∠DAE=∠GFE(錯覚)・・・?
?,?より
2組の角がそれぞれ等しく なりますから
△EGF ∽△EDA
になります。
そして、辺ADの長さが3?で、
辺GFの長さが3.5?ですから
△EGF :△EDA=3.5:3=7:6
辺EG :辺ED=7:6 になります。
△AED をUにし△AGEはSですから、
S :U=7:6・・・?
となります。

つぎに、△AEDと△CEBで考えます。
仮定により、
AD//BC ですから
∠ADE=∠CBE(錯覚)・・・?
∠DAE=∠BCE(錯覚)・・・?
?,?より
2組のそれぞれの角が等しくなりますから
△AED∽△CEB
となります。
△CEBをVとすると、
AD=3cm
BC=10cm
△AED:△CEB=3:10
AE:CE=3:10
となり、
U:V=3:10
∴ AE:CE=3:10
U:T=3:10・・・?
になります。
?,?より
S:U=7:6
U:T=3:10
2つを比べるためにUを同じくらいにします。
S:U=7:6
U:T=6:20
よって
S:T=7:20
になります。
答え 7:20








コメント