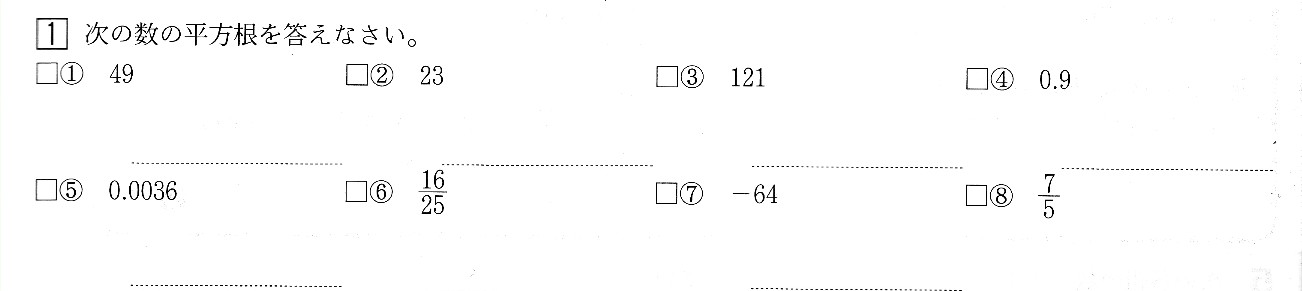
中学3年数学 三平方の定理の利用 練習問題4・解答
4、次の問いに答えてください。
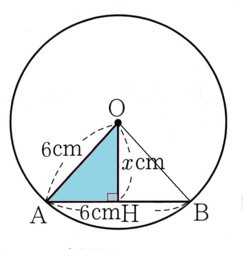
(1)半径6cmの円Oがあります。円Oの弦ABの長さが6cmのとき、中心Oから弦ABまでの距離を求めてください。
 図をかいて考えてみます。
図をかいて考えてみます。
そうすると、中心Oから弦ABまでの距離は
直角三角形の直角を挟む辺になり、もう1つの辺はAHの長さになり、半径の長さが斜辺になります。
OA(半径)=6cm
AH(底辺)=6cm÷2=3cm
OH(高さ)=χ?
三平方の定理
a²+b²=c²
3²+χ²=6²
9+χ²=36
χ²=36−9
χ=√27(χは+になります)
χ=3√3
答え OH=3√3?
(2)半径9cmの円Oで、中心からの距離が5cmであるような弦ABの長さを求めてください。
 図にかいてみましょう。
図にかいてみましょう。
円Oの半径が斜辺になる直角三角形になります。
弦ABは△OAHの辺AHを底辺と考えたとき、その2倍が弦ABの長さになります。
OA(斜辺)=9cm
OH(高さ)=5cm
AH(底辺)=χ?
三平方の定理を利用します。
(底辺)²+(高さ)²=(斜辺)²
χ²+5²=9²
χ²+25=81
χ²=81−25
χ²=56
χ=√56(χは+になります)
χ=2√14
辺AH=2√14?
辺AB=辺AH×2
辺AB=2√14×2
辺AB=4√14
答え 弦AB=4√14?
(3)円Oで、弦ABの長さが20cm、中心Oから弦ABまでの距離が24cmのとき、円Oの半径を求めてください。
 図にかいてみましょう。
図にかいてみましょう。
円Oの半径がχ?になる直角三角形になります。
高さOHが24?
斜辺OAがχ?
底辺AHが10?
の直角三角形になります。
三平方の定理を使い斜辺OAの長さを求めます。
10²+24²=χ²
100+576=χ²
676=χ²
χ=√676
χ=26(χは+になります。)
答え 半径は、26?
(4) 半径10cm、中心角120゜の扇形OABで、弦ABの長さを求めてください。
半径10cm、中心角120゜の扇形OABで、弦ABの長さを求めてください。
Oから弦ABに垂線を引きます。
この線は中心角の二等分線になりますから、
∠AOHは60゜になります。
∠OHAは90゜になります。
この直角三角形は
(底辺)=1
(斜辺)=2
(高さ)=√3
の比率になります。
10:χ=2:√3
10×√3=2×χ
10√3=2χ
2χ×1/2=10√3/2
χ=5√3
弦ABはAH+HBですから
5√3×2=10√3
答え 弦AB=10√3?










コメント