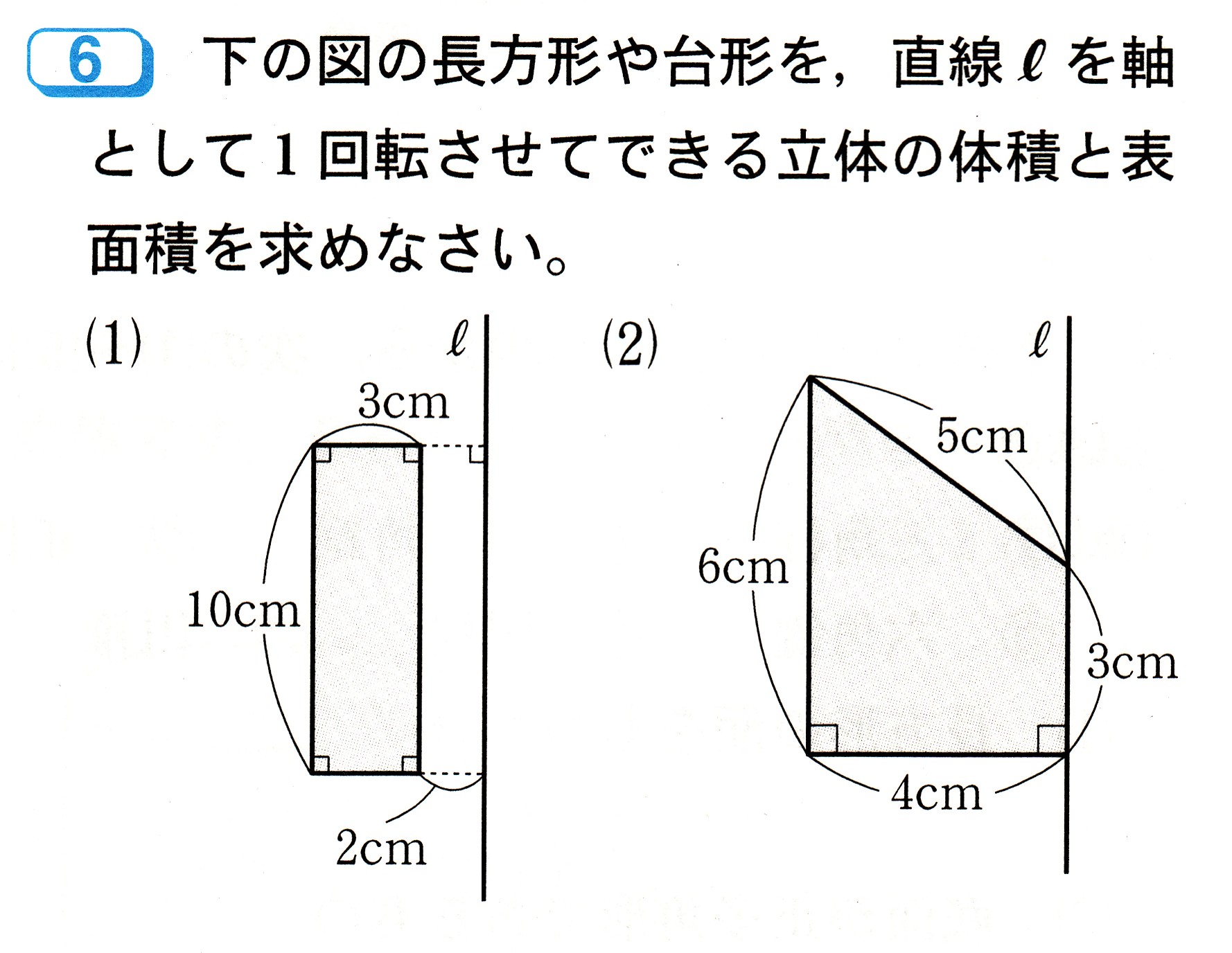
中学２年数学 円周角の定理 平面図形 確認問題５・解答
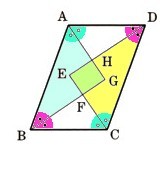
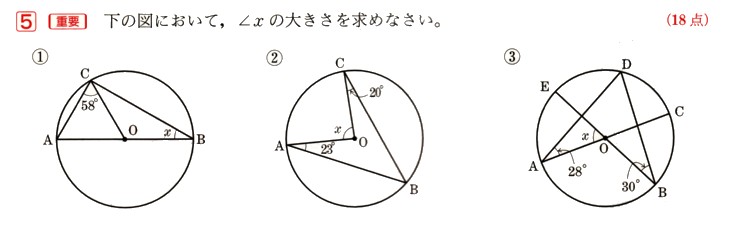
５、図において、∠χの大きさを求めてください。
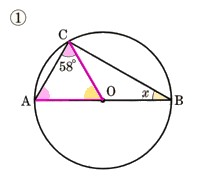
① 
まずは、弧ＡＣの中心角を求め、そこから弧ＡＣの円周角を求めます。
まずは、弧ＡＣの中心角を求め、そこから弧ＡＣの円周角を求めます。 △ＡＯＣの辺ＡＯ，ＣＯは円の半径になりますから、
ＡＯ＝ＡＣ になります。
2つの辺が等しいので、二等辺三角形の底角が∠Ａ、∠ＯＣＡということになります。
底角は等しくなりますから、∠Ａは58°ということになります。
三角形の内角の角の和は180度ですから
∠ＡＯＣ＝180°ー(58°＋58°)
＝180°ー116°
＝64°
弧ＡＣの中心角が64°とわかりました。
円周角は中心角の半分になりますから、
64°×1/2＝32°
∠ＣＢＡ＝32°
とわかりました。
答え χ＝32°
②
χの部分を求めるためにＢＯの延長に内接するように補助線を引きます。
χの部分を求めるためにＢＯの延長に内接するように補助線を引きます。 そうすると、
△ＡＯＢと△ＣＯＢの2つの内角の和の外角の和になります。
わかりにくいので、
χ＝（∠ＯＡＢ＋∠ＯＢＡ）＋（∠ＯＣＢ＋∠ＯＢＣ）
になります。
χ＝23°＋23°＋20°＋20°
＝46°＋40°
＝86°
答え χ＝86°
③ 
今回はχを求めるために、補助線をＯＤに引きます。
今回はχを求めるために、補助線をＯＤに引きます。 そして、弧ＥＤと弧ＣＤの中心角をだし、直線ＡＣから∠ＥＯＣを引けば∠χが求められます。
まずは、弧ＥＤから考えていきます。
弧ＥＤの円周角は∠ＤＢＥになりますから、
∠ＤＢＥ＝30°・・・円周角
中心角は円周角の2倍になりますから、
∠ＤＯＥ＝30°×2
＝60°
弧ＣＤを考えます。
弧ＣＤの円周角は∠ＤＡＣになりますから、
∠ＤＡＣ＝28°・・・円周角
中心角は円周角の2倍になりますから、
∠ＤＯＣ＝28°×2
＝56°
∠ＥＯＣ＝∠ＤＯＥ＋∠ＤＯＣ
＝60°＋56°
＝116°
χ＝180°ー∠ＥＯＣ
＝180°ー116°
＝64°
答え χ＝64°
コメント