中学2年数学 平面図形 まとめテスト1・解答
1、次の問いに答えてください。
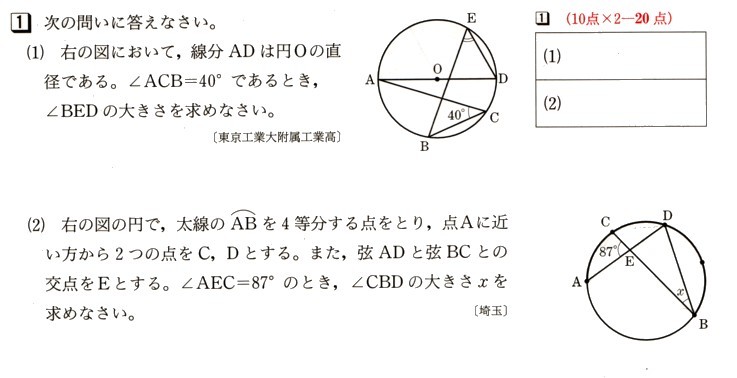
(1) 図において、線分ADは円Oの直径になります。∠ACB=40°であるとき、∠BEDの大きさを求めてください。
図において、線分ADは円Oの直径になります。∠ACB=40°であるとき、∠BEDの大きさを求めてください。
 図において、線分ADは円Oの直径になります。∠ACB=40°であるとき、∠BEDの大きさを求めてください。
図において、線分ADは円Oの直径になります。∠ACB=40°であるとき、∠BEDの大きさを求めてください。 まずは、AEを結ぶ直線をかきます。
そして,△AEDで考えます。
△AEDの∠AEDは弧ADの円周角になりますから90°になり、
∠AED=90°
△AEDは直角三角形になります。
つぎに、 弧ABで考えます。
弧ABで考えます。
 弧ABで考えます。
弧ABで考えます。 弧ABの円周角は∠ACB=40°
(弧の長さが同じであれば円周角は同じになります。)
よって,∠AEB=40° になります。
求めるのは、∠BEDですから
∠BED=∠AEDー∠AEB
=90°ー40°
=50°
∠BED=50°
答え ∠BED=50°
(2)図 の円で、太線のA⌒Bを4等分する点をとり、点Aに近い方から2つの点をC、Dとします。また、弦ADと弦BCとの交点をEとします。∠AEC=87°のとき、∠CBDの大きさを求めてください。
の円で、太線のA⌒Bを4等分する点をとり、点Aに近い方から2つの点をC、Dとします。また、弦ADと弦BCとの交点をEとします。∠AEC=87°のとき、∠CBDの大きさを求めてください。
 の円で、太線のA⌒Bを4等分する点をとり、点Aに近い方から2つの点をC、Dとします。また、弦ADと弦BCとの交点をEとします。∠AEC=87°のとき、∠CBDの大きさを求めてください。
の円で、太線のA⌒Bを4等分する点をとり、点Aに近い方から2つの点をC、Dとします。また、弦ADと弦BCとの交点をEとします。∠AEC=87°のとき、∠CBDの大きさを求めてください。 まずは、点Aと点Bを結ぶ線をかきます。
まずは、点Aと点Bを結ぶ線をかきます。 弧ADと弧DBの長さは同じですから円周角は同じ角度になります。
そうすると,△ABDの∠DABと∠DBAの角度が同じ角度になります。
2つの角度が同じですから△ABDは二等辺三角形になります。
 つぎに、∠CEA=87°について考えると、
つぎに、∠CEA=87°について考えると、 ∠CEAは、△AEBの外角になります。
∠EAB+∠EBA=∠CEA
になります。
直線CBは∠DBAの二等分線になりますから
∠DBEをχとした場合,∠EBAもχとなります。
∠DABは∠DBAと同じ角度ですから、χ×2になり
ます。
ます。
∠DAB=2χ°
 式にしてみましょう。
式にしてみましょう。 87°=2χ°+χ°
87°=3χ°
χ=29°
答え χ=29°









コメント