中学2年数学 平面図形 2まとめテスト4・解答つづき
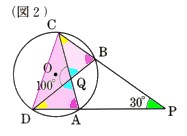
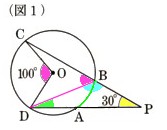
(2)図2 のように、直線ACとBDの交点をQとし、∠CQD=100°であるとき、弧ABの長さを求めてください。
のように、直線ACとBDの交点をQとし、∠CQD=100°であるとき、弧ABの長さを求めてください。
今回も弧ABの中心角から、弧ABの長さを求めていきます。
∠BCQをχ°
∠CBQをy°
として考えていきましょう。
∠CQDは、△CBQの外角になります。
∠CQD=∠BCQ+∠CBQ
100°=χ°+y°
つぎに、△CAPについて考えます。
△CAPの外角が∠CADになります。
∠CAD=∠CPA+∠PCA
∠CADは、弧CDの円周角になりますから∠CBDとも同じになります。
∠CAD=y°
∠CPA=30°
∠PCAは∠BCQ(χ°)と同じですから
∠PCA=χ°
y°=30°+χ°
になります。
つぎに、△QDAについて考えます。
∠QDAを求るために、
三角形の内角の和は180°
∠DQA=80°
∠QAD=30°+χ°
になります。
∠QDA=180°−(80°+30°+χ)
=180°−110°−χ°
=70°−χ°
そして、∠QDAは弧ABの円周角でもありますから
∠QDA=χ°
になり、
χ°=70°−χ°
χ°+χ°=70°
2χ°=70°
χ°=35°
になります。
これで、弧ABの円周角がわかりました。
弧ABの円周角=35°
中心角は円周角の2倍になりますから
35°×2=70°
弧ABの中心角が70°とわかりました。
この、1cmの円の円周の70/360 が弧ABのこの長さになります。
円周の長さは (半径)×2×π になります。
1×2×π=2π(?)
2π?×70/360
=2π?×7/36
=7π/18(?)
弧ABのこの長さがわかりました。
答え 7/18 π(?)






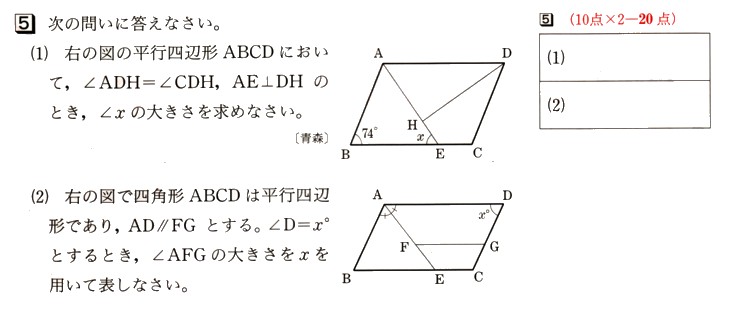
コメント