中学2年数学 2(図形・確率)まとめテスト5・解答
5、次の問いに答えてください。
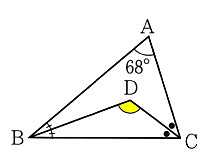
(1)図 において、点Dは∠B、∠Cの二等分線の交点になります。∠BAC=68°のとき、∠BDCの大きさを求めてください。
において、点Dは∠B、∠Cの二等分線の交点になります。∠BAC=68°のとき、∠BDCの大きさを求めてください。
 において、点Dは∠B、∠Cの二等分線の交点になります。∠BAC=68°のとき、∠BDCの大きさを求めてください。
において、点Dは∠B、∠Cの二等分線の交点になります。∠BAC=68°のとき、∠BDCの大きさを求めてください。 ●をχとし、×をyとして考えます。
△ABCで考えます。
三角形の内角の和は180度になりますから、
180=∠BAC+∠ABC+∠ACB
=68°+2y+2χ
180−68=2y+2χ
112=2χ+2y
112=2(χ+y)
56=χ+y・・・①
になります。
①より△BDCは三角形の内角の和は180°になりますから
180=χ+y+∠BDC
180=56+∠BDC
∠BDC=180−56
∠BDC=124
答え ∠BDC=124°
(2)図 で、四角形ABCDは正方形、△PBCは正三角形になります。このとき、∠APDの大きさを求めてください。
で、四角形ABCDは正方形、△PBCは正三角形になります。このとき、∠APDの大きさを求めてください。
 で、四角形ABCDは正方形、△PBCは正三角形になります。このとき、∠APDの大きさを求めてください。
で、四角形ABCDは正方形、△PBCは正三角形になります。このとき、∠APDの大きさを求めてください。 △PBCは正三角形ですからそれぞれの辺の長さは等しくなります。
PB=PC=BC・・・①
四角形ABCDは正方形ですからそれぞれの辺の長さが等しくなります。
AB=BC=CD=DA・・・②
①,②より
辺PB=辺ABになります。・・・③
 △ABPにおいて、頂角∠ABP、辺AB、辺PBになり
△ABPにおいて、頂角∠ABP、辺AB、辺PBになり △ABPは二等辺三角形になりますから底角∠BAP、∠BPAは等しくなります。
∠BAP=∠BPA・・・④
△ABPの内角の和は180°になり、頂角は30°になりますから底角は、
180=(頂角)+2×(底角)
180=30°+2(底角)
2(底角)=180−30
2(底角)=150
底角=150÷2
=75
④より、∠BAP=∠BPA=75°・・・⑤
 次に、△ABPと△DCPにおいて
次に、△ABPと△DCPにおいて 仮定により
AB=DC・・・⑥(正方形のそれぞれの辺)
PB=PC・・・⑦(正三角形のそれぞれの辺)
∠ABPは、∠ABC(90°)から∠PBC(60°)を引いた角度になります。
∠DCPは、∠DCB(90°)から∠PCB(60°)を引いた角度になります。
∠ABP=∠ABC−∠PBC
=90−60
=30°
∠DCP=∠DCB−∠PCB
=90−60
=30°
∠ABP=∠DCP・・・⑧
⑥,⑦,⑧より
2つの辺とその間の角がそれぞれ等しくなりますから
△ABP≡△DCP
合同な三角形の対応する角はそれぞれ等しくなりますから
∠APB=∠DPC
⑤より、∠APB=∠DPC=75°
∠BPCは正三角形のそれぞれの角になりますから60°となりますから。
360°=∠APD+∠APB+∠DPC+∠BPC
=∠APD+75°+75°+60°
∠APD=360−(75°+75°+60°)
=360−210
=150
答え ∠APD=150°








コメント