中学3年数学 変化の割合の計算、交点の座標
1、変化の割合の計算
○関数y=aχ²の変化の割合
χの値がpからqまで増加するとき、
変化の割合=a(p+q)
で求めることができます。
〔証明〕
関数y=aχ²において、χの値がpからqまで増加するときの変化の割合は、
χの増加量は、q−p
yの増加量は、aq²−ap²=a(q−p)
=a(q+p)(q−p)
a(q+p)(q−p)
変化の割合=―――――――――
q−p
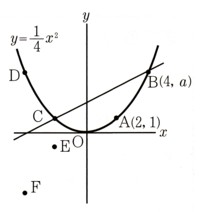
2、交点の座標
○関数y=aχ²と一次関数y=pχ+qのグラフの交点の座標は、2つの式を連立方程式と見たときの解になります、
y=aχ²
{ ⇒aχ²=pχ+qの二次方程式を解きます。
y=pχ+q
○関数y=aχ²と2点で交わる直線の傾きは、その2点間の変化の割合に等しくなります。
よって、交点のχ座標がp、qのとき、直線の傾きはa(p+q)で求めることができます。








コメント