中学3年数学 図形と相似 平行線と線分の比 3確認問題2・解答
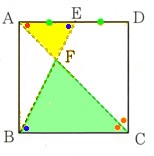
2、つぎの図 において、四角形ABCDは正方形になります。EはADの中点になり、Fは
において、四角形ABCDは正方形になります。EはADの中点になり、Fは
ACとBEの交点になります。このとき、次の問いに答えてください。
(1)EFの長さとFBの長さの比を最も簡単な整数の比で表してください。
正方形ですから、AD//BCとなります。
次に△AFE∽△CFB になります。(2組の角がそれぞれ等しい)
AEはADの中点ですから
AE:AD=1:2
となり、AD=BC ですから
△AFE:△CFB=1:2となります。
∴ EF:FB=1:2 となります。
答え 1:2
(2)四角形EFCDの面積は正方形ABCDの面積の何倍になりますか?
△AEFを基準に考えます。
△AFB:△AEF=2:1
になりますから、
△BFC:△AFB=4:2
で、△ABC:△AEF=6:1
になります。
△ABC=△ADCですから
△AEF:△ADC=1:6
∴四角形EFCDは△AEFを1と考えると
△AEF:四角形EFCD=1:5
四角形全体を12と考えると
12:5=四角形ABCD:四角形EFCD
四角形EFCD×12=四角形ABCD×5
四角形EFCD=四角形ABCD×5×1/12
四角形EFCD=四角形ABCD5/12
四角形EFCDは四角形ABCDの5/12となります。
答え 5/12倍






コメント