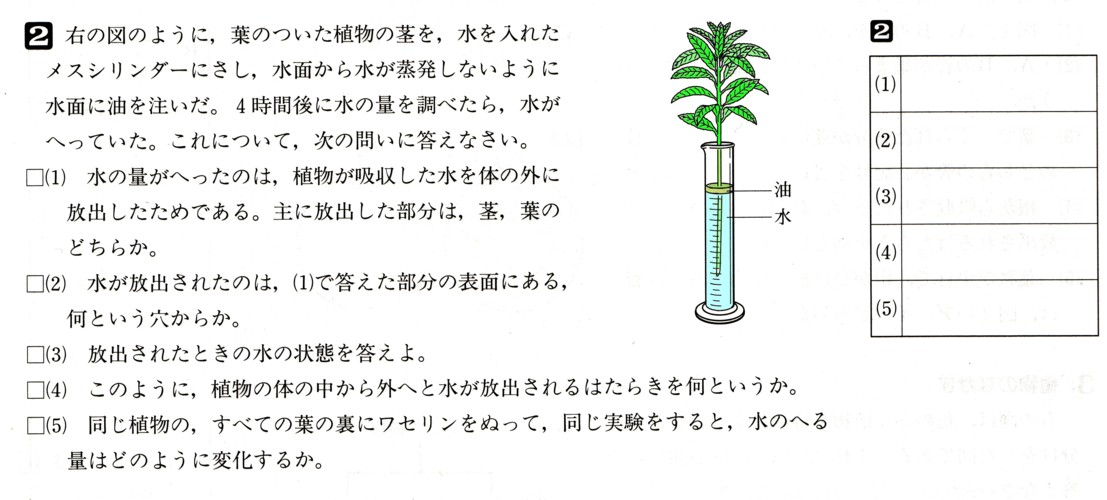
中学3年数学　三平方の定理の利用　練習問題６・解答

中学3年数学　三平方の定理の利用　練習問題６・解答

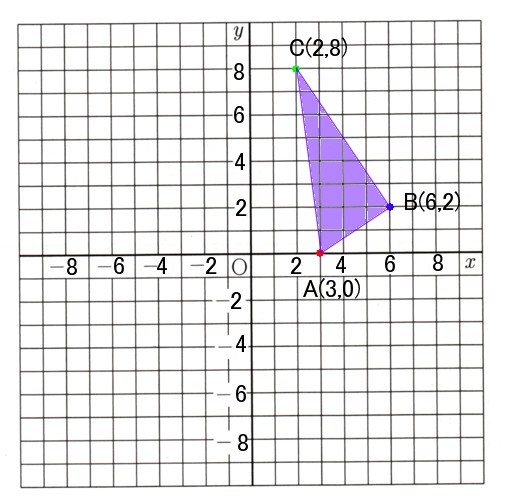
６、△ＡＢＣの各頂点の座標は、Ａ（３，０），Ｂ（６，２），Ｃ（２，８）になります。

このとき、次の問いに答えてください。

（１）各辺の長さを求めてください。

公式を使って考えましょう。

ＡＢ＝√（χ₁−χ₂）²＋（ｙ₂−ｙ₁）²

Ａ（３，０），Ｂ（６，２）

ＡＢ＝√（６−３）²＋（２−０）²

ＡＢ＝√３²＋２²

ＡＢ＝√９＋４

ＡＢ＝√１３

答え　ＡＢ＝√１３

Ｂ（６，２），Ｃ（２，８）

ＢＣ＝√（２−６）²＋（８−２）²

ＢＣ＝√（−４）²＋６²

ＢＣ＝√１６＋３６

ＢＣ＝√５２

2)52
2)26
  13

ＢＣ＝２√１３

答え　ＢＣ＝２√１３

Ｃ（２，８）、Ａ（３，０）

ＣＡ＝√（３−２）²＋（０−８）²

ＣＡ＝√１²＋（−８）²

ＣＡ＝√１＋６４

ＣＡ＝√６５

5)65
  13

答え　ＣＡ＝√６５

（２）△ＡＢＣはどんな三角形になりますか？

ＡＢ＝√１３

ＢＣ＝２√１３

ＣＡ＝√６５

この場合は三平方の定理を使って直角三角形かをたずねています。

ですから、一番長くなる辺を斜辺を考え三平方の定理が成立するのかを考えます。

ＡＢ＝√１３

ＢＣ＝√５２

ＣＡ＝√６５

ＣＡを斜辺と考え式を作っていきます。

ＡＢ²＋ＢＣ²＝ＣＡ²

（√１３）²＋（２√１３）²＝１３＋４×１３＝１３＋５２＝６５

（√６５）²＝６５

式が成立しますから。この△ＡＢＣは直角三角形ということがわかります。

答え　∠Ｂ＝９０゜の直角三角形