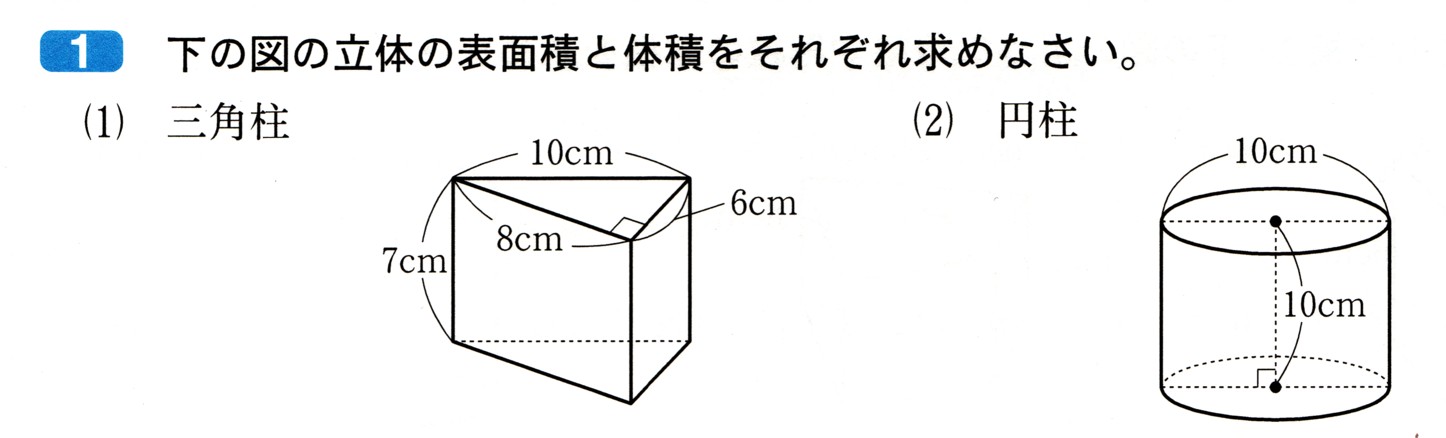
中学３年数学 関数ｙ＝ａχ²の値の変化 練習問題８・解答
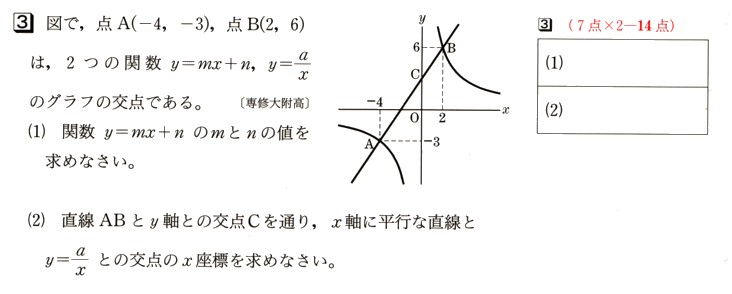
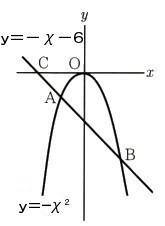
８、次の図
のように、関数ｙ＝−χ²のグラフに直線ｙ＝−χ−６が２点Ａ，Ｂで交わっています。また、ｙ＝−χ−６がχ軸と交わる点をＣとします。このとき、次の問いに答えてください。
（１）点Ｃの座標を求めてください。
点Ｃの座標を求めるために直線ｙ＝−χ−６にｙ＝０を代入します。
０＝−χ−６
−χ＝０＋６
χ＝−６
答え (χ、ｙ)＝（−６，０）
（２）２点Ａ，Ｂの座標を求めてください。
２つのグラフの式を連立方程式にして考えます。
ｙ＝−χ²
｛
ｙ＝−χ−６
(代入法)
−χ²＝−χ−６
−χ²＋χ＝−６
(二次方程式)
−χ²＋χ＋６＝０
χ²−χ−６＝０
となります。
乗法公式を使い因数分解をします。
○χ²＋χ（ａ＋ｂ）＋ａｂ＝（χ＋ａ）（χ＋ｂ）
χ²−χ−６＝０
かけて−６、足して−１になる２つの数は
−３×２＝−６、−３＋２＝−１
χ²−χ−６＝（χ−３）（χ＋２）
（χ−３）（χ＋２）＝０
○Ａ×Ｂ＝０ならば、Ａ＝０ または Ｂ＝０ になります。
χ−３＝０ 、χ＋２＝０
χ＝３ 、 χ＝−２
これで、２つの点Ａ，Ｂのχの座標がわかりました。
点Ａは、グラフを見ると負の数となりますから、−２ということがわかり、
点Ｂは、グラフを見ると正の数となりますから、３となります。
次に、ｙ＝−χ−６ の式にχ＝−２、χ＝３を代入していきます。
ｙ＝−（−２）−６ 、ｙ＝−３−６
ｙ＝２−６ 、ｙ＝−９
ｙ＝−４
点Ａは（χ、ｙ）＝（−２、−４）
点Ｂは（χ、ｙ）＝（３、−９）
となることがわかりました。
答え
点Ａは（χ、ｙ）＝（−２、−４）、点Ｂは（χ、ｙ）＝（３、−９）
（３）△ＡＯＢの面積を求めてください。ただし、１目盛りを１ｃｍとします。
直線ＡＢがｙ軸に接した部分を点Ｃとして、
△ＡＯＢは△ＡＯＤと△ＢＯＤを足したものと考えます。
点Ｄはｙ＝−χ−６の切片になりますから、
点Ｄの座標は（χ、ｙ）＝（０、−６）になります。
△ＡＯＤの底辺をＯＤと考えると、６?になります。
高さは、点Ａのχ座標になりますから、２cmとなり、
三角形の面積は、６×２÷２＝６㎠ になります。
次に△ＢＯＤを考えます。
底辺は同じように６?になります。
高さは、点Ｂのχ座標になりますから3cmになります。
三角形の面積は、6×３÷2＝９㎠
△AOＤ＋△BOＤ＝△AOB
（６㎠）＋（９㎠）＝１５㎠
答え １５㎠
コメント