中学1年数学 直線図形と対称 基本の作図 確認問題6 解答・解説
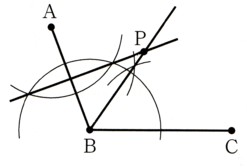
図に3点A,B,Cが与えられています。これを用いて、次の[ ]の中の
条件?,?をともに満たす点Pを、定規とコンパスを使って作図してください。
[ ?∠ABP=∠CBP ?AP=BP ]
まずは、(点A、点B)、(点B、点C)を直線でつなげます。
これで、∠ABCの角度がわかりました。∠Bの二等分線がわかれば、この線上
に点Pがあると考えれば。
∠ABP=∠CBPと言うことがわかります。
それでは∠Bの二等分線を作図しましょう。
点Bを中心に適当な半径の円をかきます。その円と辺AB、辺BCの接点を
中心に半径の同じ円を2つかきます。その2つの円の交点が二等分線になります。
これで、∠ABP=∠CBPの条件をクリアしました。つぎにAP=BPです。
AP=BPということは、辺ABの垂直二等分線であれば、点Aと点Bの線分に
なにます。この線分上に点Pがあります。そうすると、点Pを頂点にした同じ
三角形ができます。この三角形は二等辺三角形になりますから、底辺ABにした
とき、辺AP,辺BPが等しいということになります。
それでは、垂直二等分線を作図してみましょう。
点A、点Bを中心に半径が同じの円をかきます、その2つの円の2つの接点を
直線でつなげます。これで垂直二等分線ができました。
∠Bの二等分線と辺ABの垂直二等分線の接点が条件を満たした点Pに
なります。









コメント