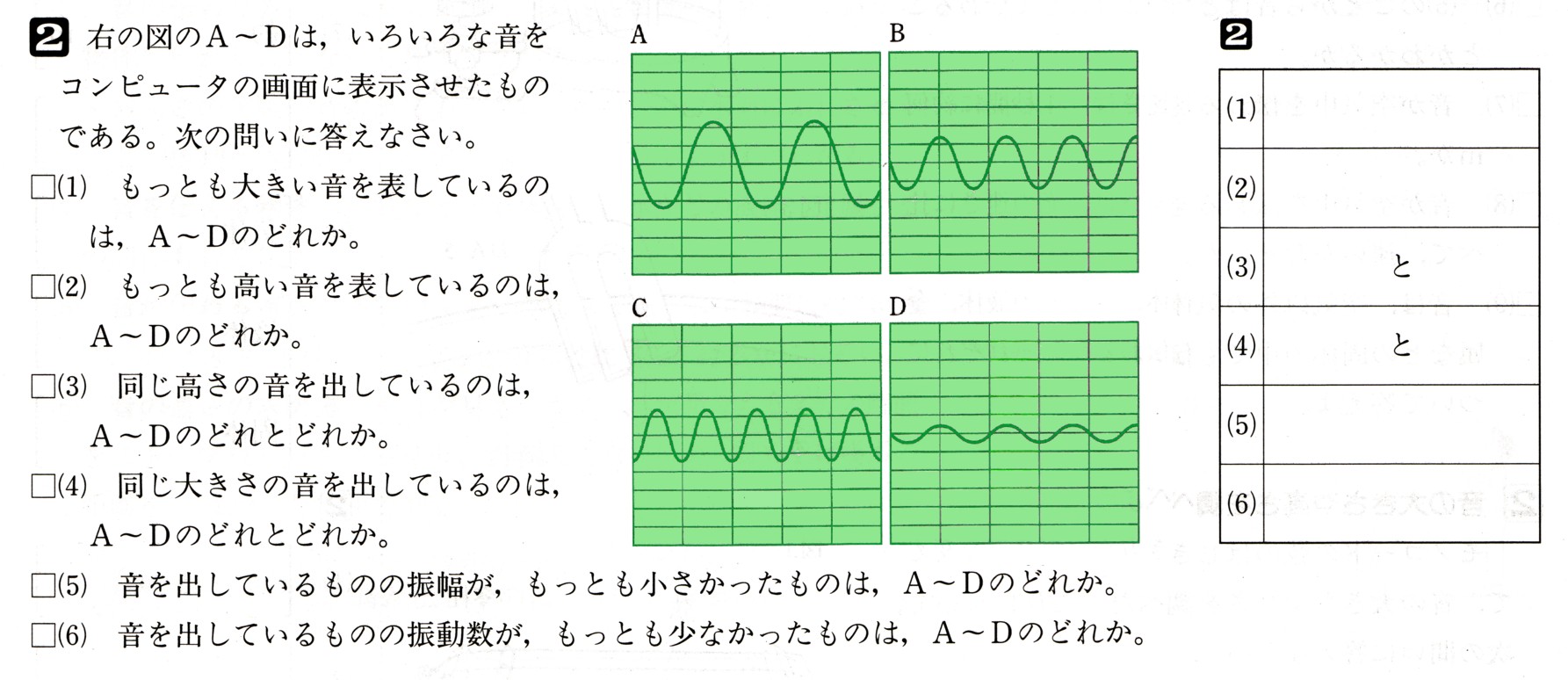
中学2年数学 平面図形 三角形の性質 確認問題2・解答
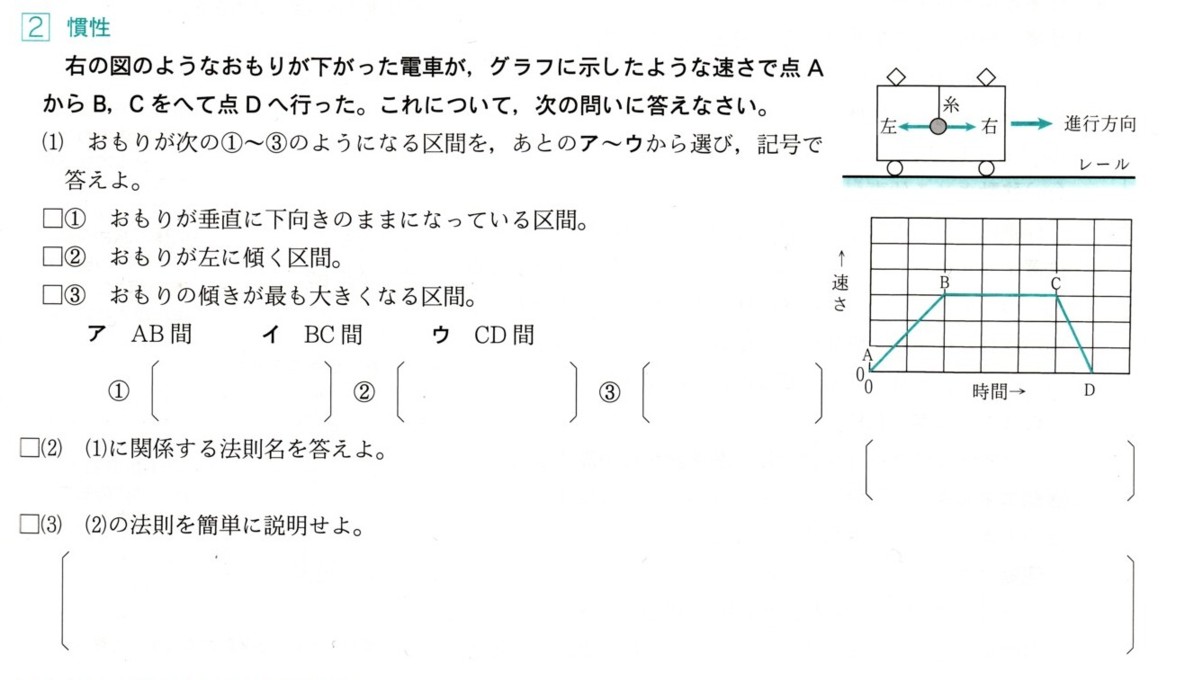
2、AB=ACである△ABCの∠Aの二等分線と辺BCとの交点をDとし、Dから2辺AB,ACにそれぞれ垂線DE、DFを引くとき、BE=CFであることを証明してください。

答え
〔証明〕
△BEDと△CFDにおいて
仮定より
頂角の二等分線は、底辺を垂直に2等分しますから
BD=CD・・・・1
△ABCはAB=ACですから二等辺三角形になります。
二等辺三角形は2つの底角がそれぞれ等しくなりますから、
∠B=∠C・・・・2
∠BED=90°
∠CFD=90°
により、
△BEDと△CFDは、直角三角形になります。
1,2より
直角三角形は、斜辺とその他の角がそれぞれ等しくなります。
よって、
△BED≡△CFD
になります。
合同な三角形の対応する辺はそれぞれ等しくなりますから
BE=CF
になります。










コメント