中学2年数学 平面図形 三角形の性質 確認問題4・解答
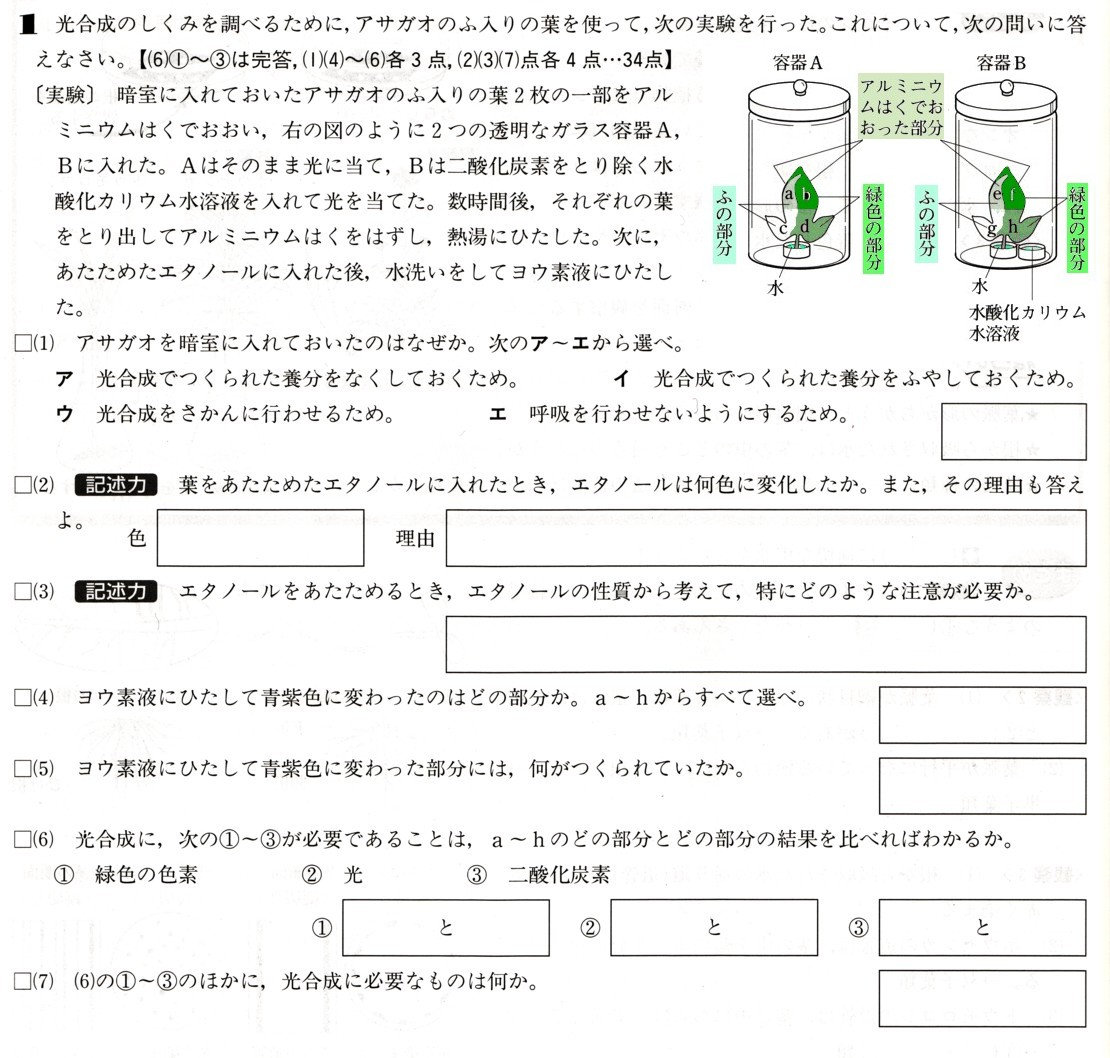
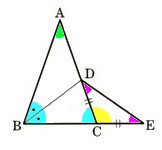
4、AB=ACである△ABCの∠Bの二等分線と辺ACとの交点をDとします。BCの延長上にCD=CEとなる点Eをとるとき、△DBEは二等辺三角形であることを証明してください。

答え
〔証明〕
まずは、△ABCで考えます。
△ABCは仮定より
AB=ACですから
二等辺三角形になります。
二等辺三角形は2つ底角がそれぞれ等しくなりますから、
∠ABC=∠ACBになります。・・・①
次に、∠DBCについて考えます、
∠DBCは、∠ABCの半分の角度になります。
∠DBC=∠ABC×1/2・・・②
つぎに、∠DECについて考えます。
仮定により
CD=CE
ですから、△CDEは二等辺三角形ということがわかります。
∠Dと∠Eが、底角になります。
△CDEの外角が∠ACBになりますから、∠Dと∠Eは、∠ACBの半分ずつになります。
∠E=∠ACB×1/2・・・③
△DBEで考えると、
∠DBC=∠ABC×1/2
∠DEC=∠ACB×1/2
ですから、①により
∠DBC=∠DEC
になりますから
△DBEの2つの底角がそれぞれ等しくなりますから、
△DBEは二等辺三角形ということがわかります。







コメント