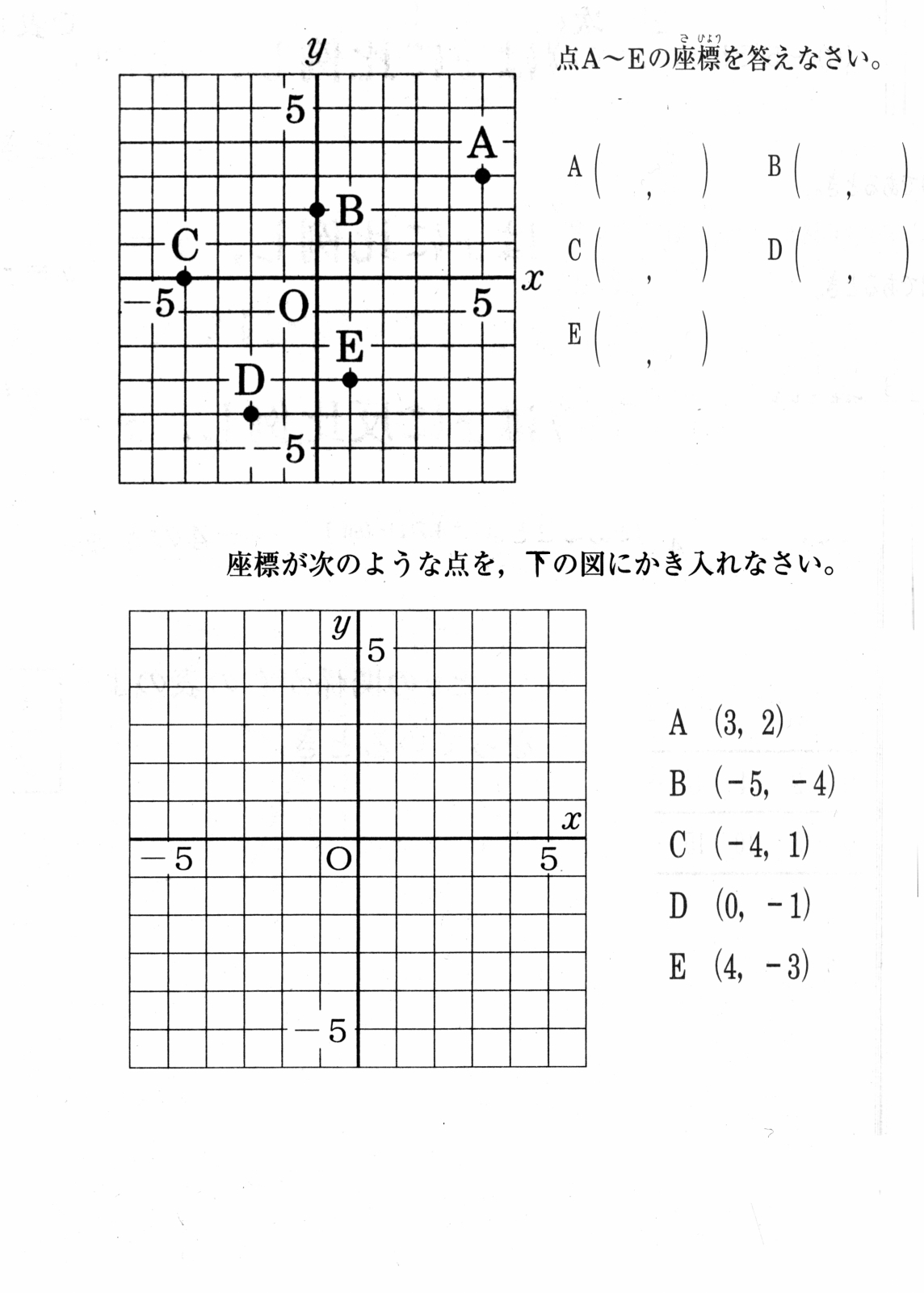
中学3年数学 式の展開と因数分解 因数分解 2確認問題3・解答
3、次の式を因数分解してください。
①,a²bーbc²
共通因数を探します。
共通因数はbになります。
b(a²ーc²)
乗法公式を利用します。
●a²ーb²=(a+b)(aーb)
(a²ーc²)=(a+c)(aーc)
b(a²ーc²)=b(a+c)(aーc)
答え b(a+c)(aーc)
②,3χ²+3χー60
共通因数を探します。
共通因数は3になります。
3(χ²+χー20)
乗法公式を利用します。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
(χ²+χー20)
かけて(ー20)「1×(−20)、2×(−10)、4×(−5)、5×(−4)、10×(−2)、20×(−1)・・・」
たして1 「5+(−4)」
(χ²+χー20)=(χ+5)(χー4)
3(χ²+χー20)=3(χ+5)(χー4)
答え 3(χ+5)(χー4)
③,ー2a²ー14aー12
共通因数を探します。
共通因数はー2になります。
ー2a²ー14aー12=−2(a²+7a+6)
乗法公式を利用します。
●χ²+(a+b)χ+ab=(χ+a)(χ+b)
(a²+7a+6)
かけて6 「1×6、2×3、3×2、6×1」
たして7 「1+6」
(a²+7a+6)=(a+1)(a+6)
−2(a²+7a+6)=−2(a+1)(a+6)
答え −2(a+1)(a+6)
④,9χy²ー16χ
共通因数を探します。
共通








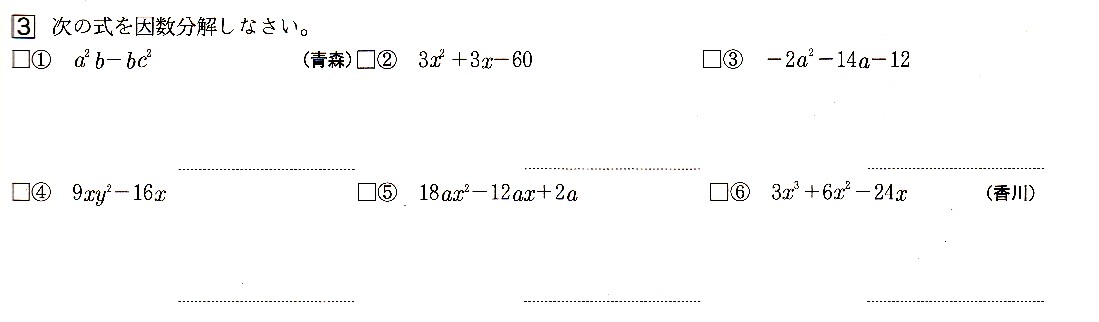

コメント