 合同
合同 中学2年数学 平面図形 平行四辺形の性質 確認問題3・解答
中学2年数学 平面図形 平行四辺形の性質 確認問題3・解答3、平行四辺形ABCDの辺AB、BC、DA上に、点P、Q、R、Sをとり、AP=BQ=CR=DSとするとき、四角形PQRSは平行四辺形となることを証明してください。 〔解説〕 △APS...
 合同
合同 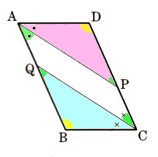 合同
合同 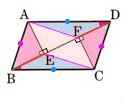 合同
合同 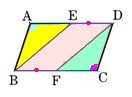 数学
数学 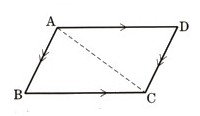 合同
合同  平面図形
平面図形  平面図形
平面図形  数学
数学  合同
合同  合同
合同