中学2年数学 図形の調べ方 2まとめテスト4・解答
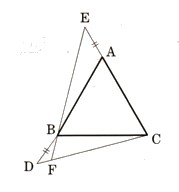
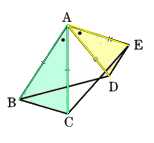
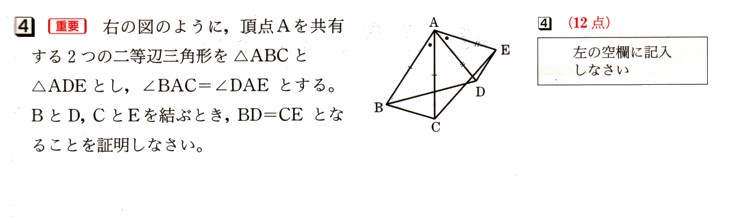
4、図 のように、頂点Aを共有する2つの二等辺三角形を△ABCと△ADEとし、∠BAC=∠DAEとします。
のように、頂点Aを共有する2つの二等辺三角形を△ABCと△ADEとし、∠BAC=∠DAEとします。
BとD、CとEを結ぶとき、BD=CEとなることを証明してください。
答え
〔証明〕

△ABDと△ACEにおいて
仮定により
∠BAC=∠DAE
∠BAD=∠BAC+∠CAD
∠CAE=∠DAE+∠CAD
よって、
∠BAD=∠CAE・・・①

△ABCと△DAEは二等辺三角形ですから
AB=AC・・・②
AD=AE・・・③
①、②、③より
2つの辺とその間の角がそれぞれ等しくなります。
よって、

△ABD≡△ACE
になり、合同な三角形の対応する辺はそれぞれ等しくなりますから
BD=CE
になります。









コメント