中学３年数学　二次方程式　２まとめテスト５・解答

中学３年数学　二次方程式　２まとめテスト５・解答

問題はこちらへ

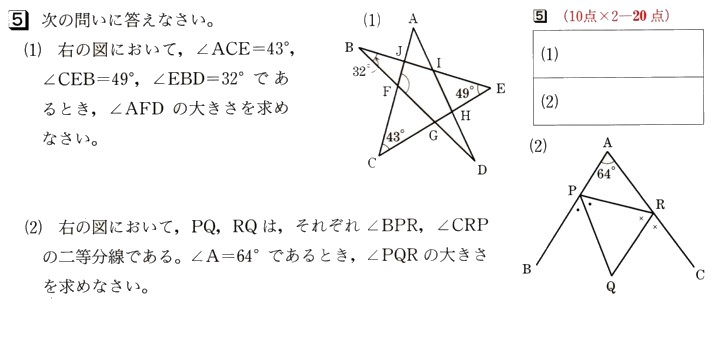
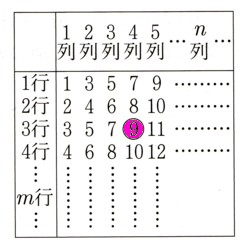
５　上の表は自然数を規則的に並べたものになります。横に並んだ数を上から1行，2行・・・とし、縦に並んだ数を左から1列，2列・・・とします。一般にm行n列にある数を（m,n）と表せば，表の○印の9は（3,4）と表せます。（m,3）の数と（m,6）の数の積が160となるとき，mの値を求めてください。

（m,3）を①
（m,6）を②
とすると

①×②＝160・・・③
表を見ると

n列は1から始まり、左に行くごとに2ずつ増えます。
m行も1から始まる、下に行くごとに1ずつ増えます。

m行の1行目のn列の値を式に表すと、2n-1となります。
※nにそれぞれの値を代入して検算してみて下さいね！

n列を求める式にm行目の数を加えれば、交点の数になります。

2n-1+m=（表の交点の数）

①（m,3）と②（m,6）を代入します。

①・・・2×3-1+m=m+5

②・・・2×6-1+m=m+11

③の式をつくります。

(m+5)(m+11)=160

乗法公式を利用して(m+5)(m+11)の展開をします。

(x+a)(x+b)=x²+(a+b)x+ab

(m+5)(m+11)=m²+(5+11)m+5×11

        　　　 =m²+16m+55

m²+16m+55=160

m²+16m+55-160=0

m²+16m-105=0

二次方程式を解くため、因数分解をします。

掛けて-105，足して16になる２つの数は

21×(-5)＝-105、21+(-5)＝16

m²+16m-105=(m+21)(m-5)

(m+21)(m-5)=0

m=-21,5

m=-21は問題の条件に合いませんから

m=5

検算してみます。

問題の表で、(5,3)と(5,6)の交点の数の積が160となります。

(5,3)の交点の数を求めます。

交点を求める式、2n-1+mに代入します。

2×3-1+5=10

同じようにして、(5,6)の交点の数も求めます。

2×6-1+5=16

③の式に代入します。

10×16=160

答えが合っていることが確認できました。

答え　ｍ＝５