二次方程式の解の公式を考えます。
両辺をaで割ります。
数の項を移行します。
xの係数の半分の2乗を両辺に足します。xの係数とは、のことです。
左辺を平方の形にして,右辺を通分します。
これから、
よって、
問題のア〜オは以下のようになります。
ア:
イ:
ウ:
エ:
オ:
問題はこちら
 数学
数学 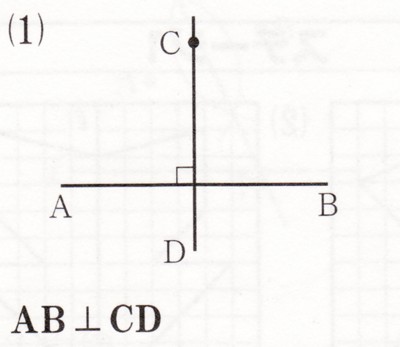 数学
数学  平面図形
平面図形  エネルギー
エネルギー  名刺の修飾
名刺の修飾  数学
数学 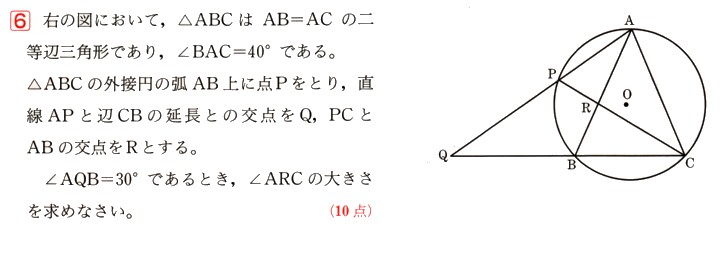 平面図形
平面図形  数学
数学 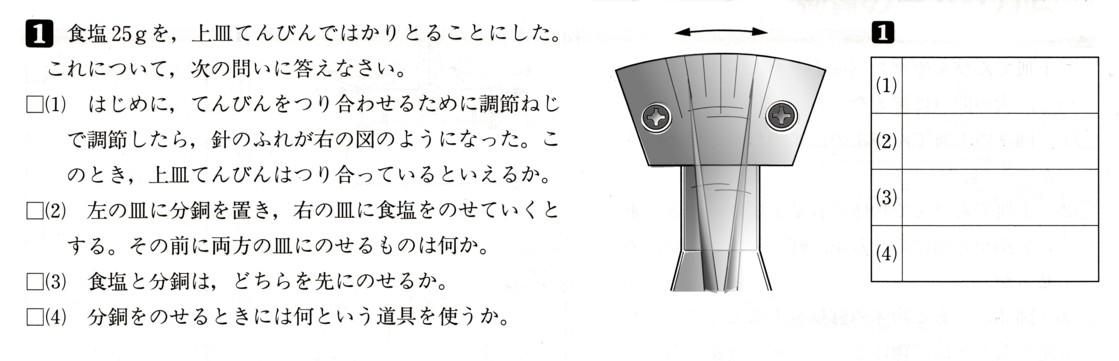 物質
物質  数学
数学  水溶液
水溶液 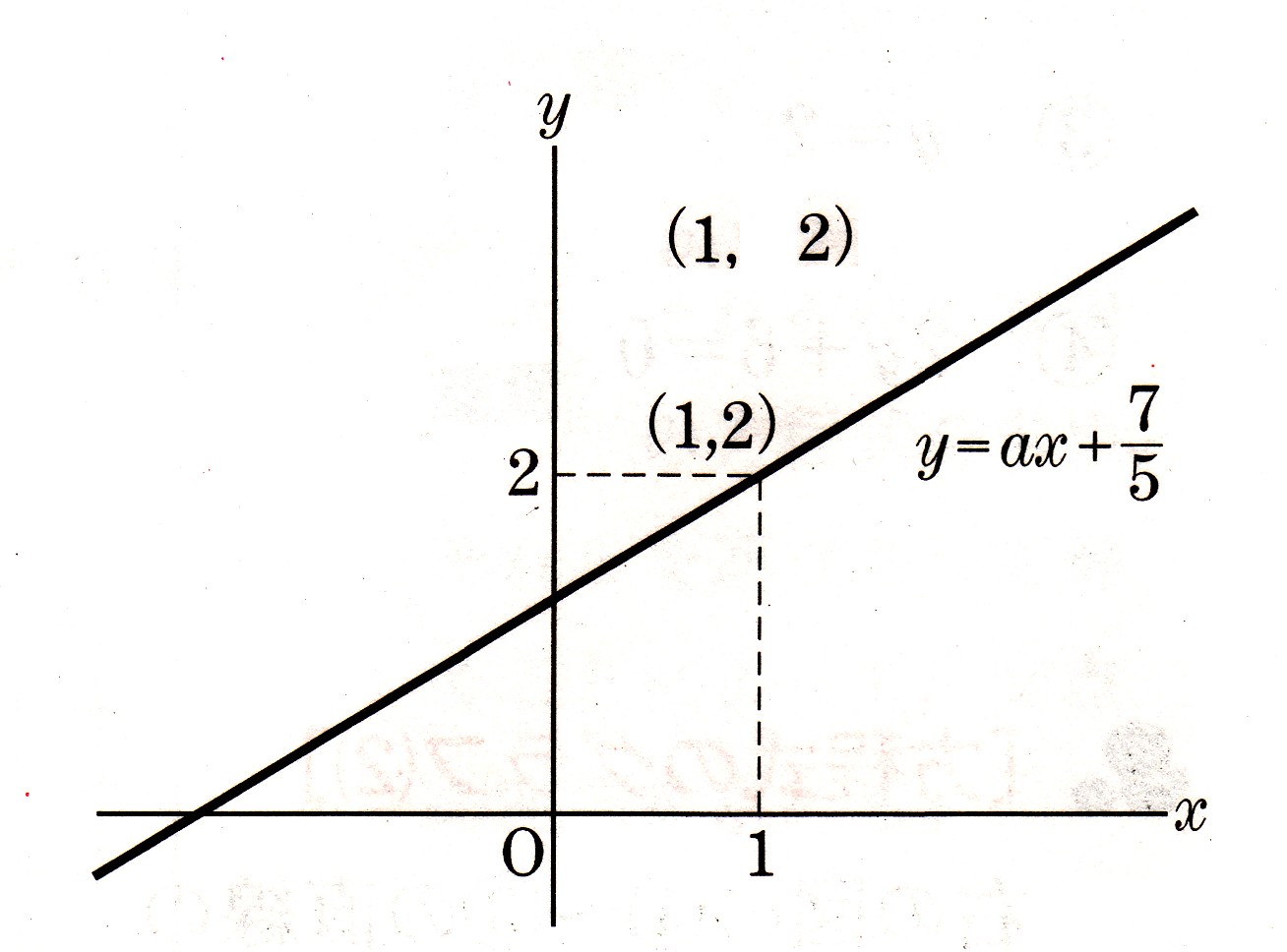 数学
数学 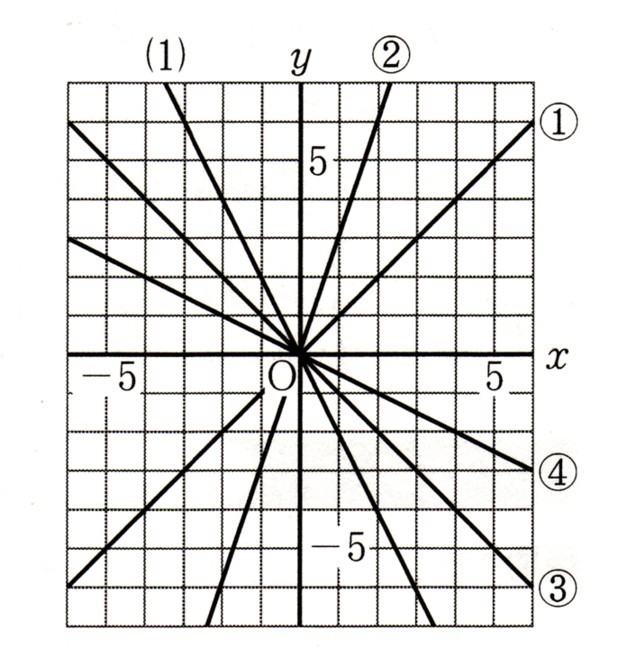 数学
数学 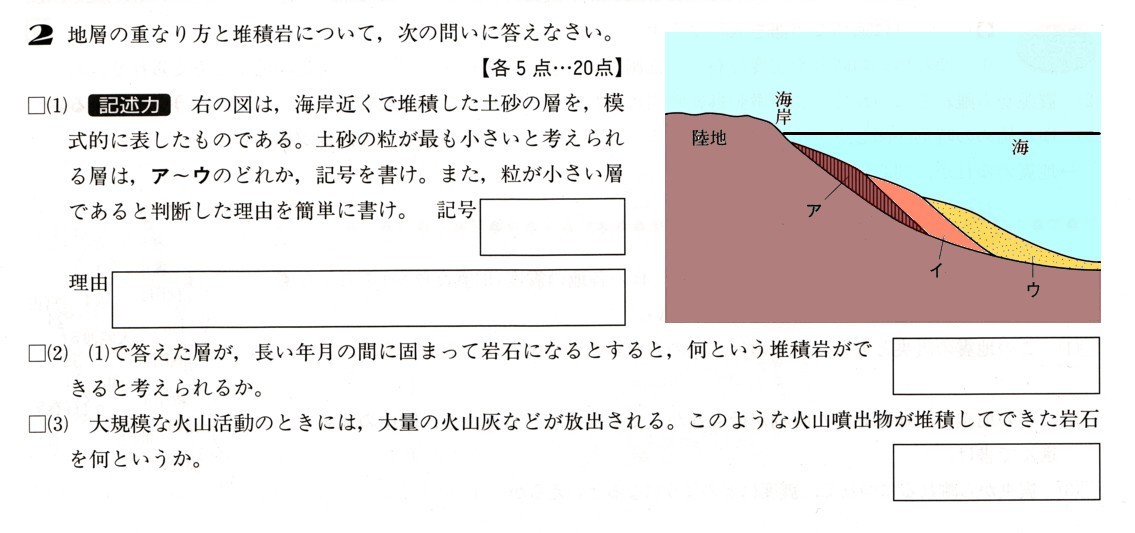 大地
大地  数学
数学 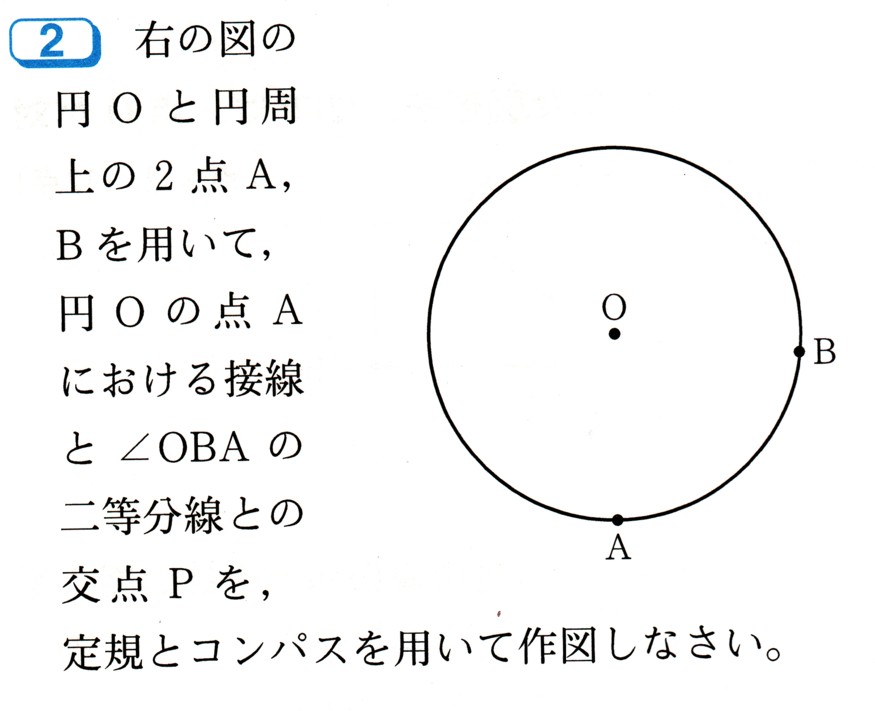 おうぎ形
おうぎ形  植物
植物 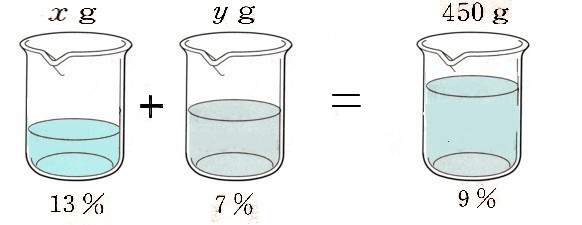 数学
数学
コメント