中学３年数学　三平方の定理　練習問題４・解答

中学３年数学　三平方の定理　練習問題４・解答

４、次の問いに答えてください。

（１）次の長さを３辺とする三角形のうち、直角三角形はどれになりますか？

記号で答えて下さい。

直角三角形の場合、ａ²＋ｂ²＝ｃ²　の式が成り立ちます。

このことにより、ａ²＋ｂ²＝ｃ²ならば、直角三角形になるということがわかります。

直角三角形の斜辺が一番長く なることがわかります。

ア 、９ｃｍ、１２ｃｍ、１５ｃｍ

一番長くなるのは１５? ですから、ｃは１５ｃｍと考えます。

９²＋１２²＝１５²

８１＋１４４＝２２５

でこの式が成り立ちますから、

直角三角形 になります。

イ、４ｃｍ、５ｃｍ、６ｃｍ

一番長くなるのは6cmになりますから、ｃが斜辺になります。

４²＋５²＝６²

１６＋２５＝41

この式は、成り立ちませんので

直角三角形にはなりません。

ウ、√３?、３ｃｍ、√６cm

√３?、√9cm、√６cm

一番長くなるのは√9?ですから、斜辺は√9?になります。

（√３）²＋（√６）²＝（√9）²

３＋６＝９

この式が成り立ちますから、

直角三角形になります。

エ、３ｃｍ、３√2?、3ｃｍ

一番長くなるのは3√2が斜辺になりますから、

３²＋３²＝（３√2）²

（3√2）²＝９×２＝１８

９＋９＝１８

この式が成り立ちますから、

直角三角形になります。

オ、3ｃｍ、7,2cm、7,8?

一番長くなるのは7,8ですから斜辺になります。

３²＋（7.2）²＝（7.8）²

９＋51,84＝60.84

この式が成り立ちますから、

直角三角形になります。

カ、1/3cm、1/4cm、1/5cm

一番長くなるのは1/3で斜辺になります。

（1/4）²＋（1/5）²＝（1/3）²

（1/4）²＋（1/5）²＝1/16＋1/25＝４１/４００

（1/3）²＝1/9

この式は、成り立ちませんので

直角三角形にはなりません。

答え　ア、ウ、エ、オ

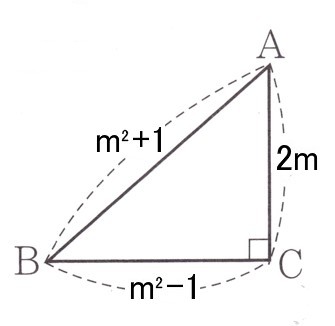
（２）３辺の長さが、m²＋１、2m、m²−１である三角形は、直角三角形であることを証明してください。

ただし、mは正の数とします。

答え

一番長くなるのは（m²＋１）になりますから、斜辺（＝ｃ）になります。

三平方の定理の式、（ａ²＋ｂ²＝ｃ²）に当てはめて考えて見ます。

直角三角形とするならば、直角に挟まれる2辺は2m、m²−１になります。

（2m）²＋（m²−１）²＝（m²＋１）²

（2m）²＝４m²

（m²−１）²＝（m²−１）（m²−１）
＝m⁴−m²−m²＋１
＝m⁴−2m²＋１

（m²＋１）²＝（m²＋１）（m²＋１）
＝m⁴＋m²＋m²＋１
＝m⁴＋2m²＋１

４m²＋m⁴−2m²＋１＝m⁴＋2m²＋１

式が成り立ちますので、直角三角形ということがわかります。