中学2年　1次関数　1次関数のグラフと式の求め方

中学2年　1次関数　1次関数のグラフと式の求め方

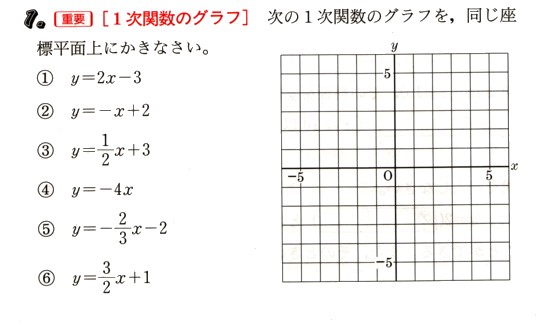
1次関数のグラフ

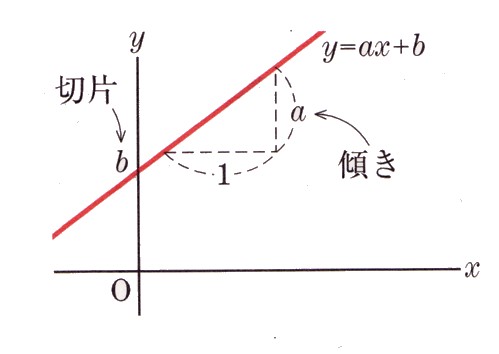
　　1次関数　y＝aχ＋b　のグラフは、ｙ＝ａχのグラフをｙ軸の正の方向にｂだけ平行移動した直線になります。

　直線　ｙ＝ａχ＋ｂ　で　ａ　を傾き、ｂを切片といいます。

1次関数の式の求め方

　　（１）傾きａ　、切片ｂ　の直線

　　　　　ｙ＝ａχ＋ｂ

　　（２）傾きｍで点(χ₁、ｙ₁)を通る直線

　　　　　ｙ＝ｍχ＋ｂ　として、χ＝χ₁、ｙ＝ｙ₁　を代入してｂを求めます。

　　（３）2点(χ₁、ｙ₁)、(χ₂、ｙ₂)を通る直線

　　　　?傾きを求める方法

　　　　　    　ｙ₂−ｙ₁　　　　   ｙの増加量
　ｍ＝――――――　(＝――――――)   から   
　　　　　    χ₂−χ₁　　　　χの増加量   　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

                                                 傾きを求めます。

　　　そして　ｙ＝ｍχ＋ｂ　に1点の座標を代入してｂを求めます。

　　　　➁連立方程式による方法

　　　ｙ＝ａχ＋ｂ　に2点の座標を代入して、ａ、ｂについての連立方程式をつくり、ａ、ｂを求めます。